Premium Only Content
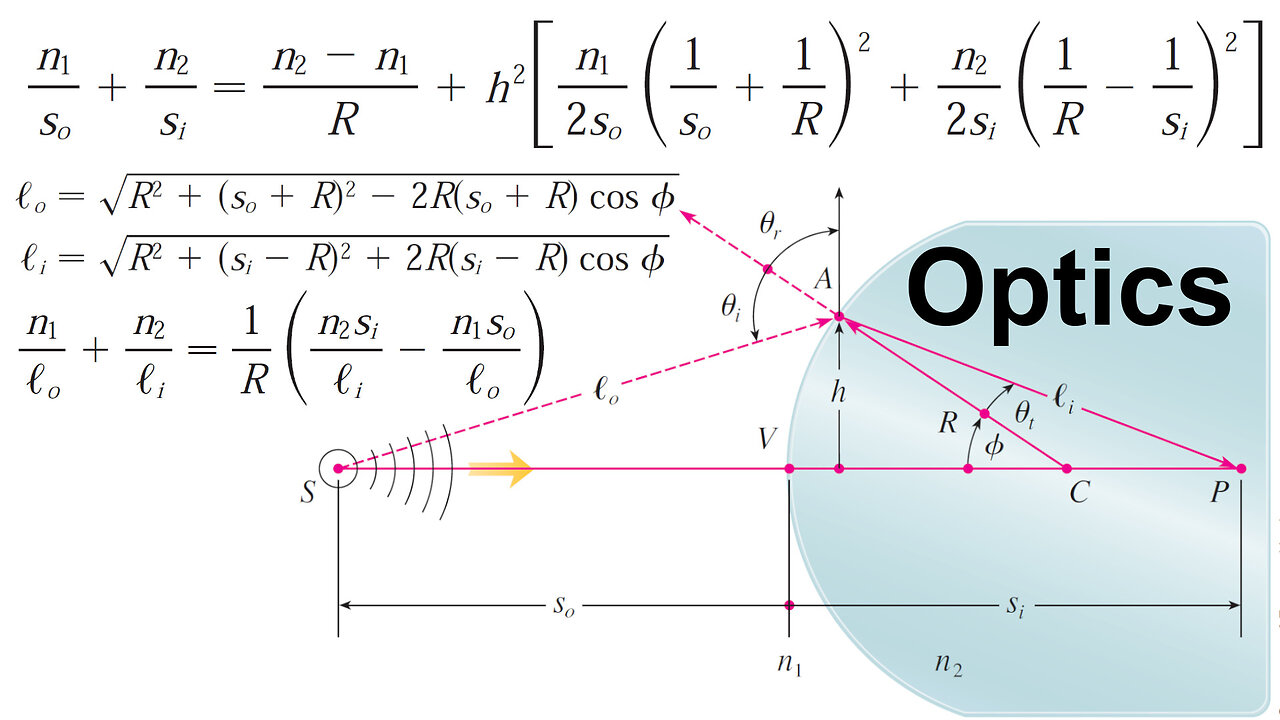
Exercise 2: Deriving the 1st Order and 3rd Order Optics Formulas
In this video, I derive the first-order and third-order optics formulas by approximating the refraction formula for light using first and third-order Taylor polynomials, respectively. Refraction refers to the change in the direction of light as it passes between different mediums due to a change in speed. Light naturally travels in a way that minimizes time, and this principle helps us derive formulas for how light refracts when entering a material. The distances light travels before and after passing through an optical lens can be calculated using the Law of Cosines, which leads to a complex equation. However, we simplify this equation using Taylor polynomial approximations.
In the first part of the video, I derive the first-order, or Gaussian optics, formula by approximating the cosine function in the distance equations with its first term, which is simply 1.
In the second part, I derive the third-order Gaussian optics formula by using the third-degree Taylor polynomial for cosine, which includes the first two non-zero terms. I also apply a given hint to approximate the inverse of the distances using the first two terms of their respective binomial series. Additionally, I use a second hint to approximate the angle with its sine, which introduces a term involving the height. After working through the algebra, I arrive at the third-order optics formula!
Timestamps:
- Exercise 2: Derive 1st Order and 3rd Order Optics Equations for refraction: 0:00
- Solution to (a): Approximating cosine with First degree Taylor Polynomial: 0:59
- Equation 3: Gaussian optics or 1st order formula: 8:26
- Solution to (b): Approximating cosine with Third degree Taylor Polynomial: 9:19
- Modifying lengths in form of Binomial series: 17:46
- 1st Hint: Approximate lengths using first 2 terms of Binomial series: 23:20
- Plugging in our approximations into Equation 1: 28:06
- 2nd Hint: Approximate ɸ with sin(ɸ) to include the height term: 43:48
- Equation 4: 3rd order optics formula: 46:37
Full video, notes, and playlists:
- Full video and playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0F76sIU8xm09oqBTq1mlry3
- HIVE notes: https://peakd.com/hive-128780/@mes/infinite-sequences-and-series-applications-of-taylor-polynomials
- Infinite Sequences and Series: https://www.youtube.com/playlist?list=PLai3U8-WIK0EXHAJ3vRg0T_kKEyPah1Lz .
------------------------------------------------------
Become a MES Super Fan! https://www.youtube.com/channel/UCUUBq1GPBvvGNz7dpgO14Ow/join
DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate
SUBSCRIBE via EMAIL: https://mes.fm/subscribe
MES Links: https://mes.fm/links
MES Truth: https://mes.fm/truth
Official Website: https://MES.fm
Hive: https://peakd.com/@mes
Email me: contact@mes.fm
Free Calculators: https://mes.fm/calculators
BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm
Free Online Tools: https://mes.fm/tools
iPhone and Android Apps: https://mes.fm/mobile-apps
-
 1:39:28
1:39:28
Math Easy Solutions
14 days ago $0.01 earnedMES Livestream 62: Nancy and John Hutchison Frequency Cannabis
4711 -
 LIVE
LIVE
Pepkilla
8 hours agoDouble XP Zombies and Warzone ~
1,816 watching -
 0:46
0:46
Dr Disrespect
2 days agoIt's not just a stream... it's an experience
481K2.82K -
 1:28:27
1:28:27
Kim Iversen
1 day agoBOMBSHELL: Secret British Military Plot to Prolong the Ukraine War And Take Down The Grayzone
89K86 -
 11:54
11:54
Professor Nez
6 hours ago🚨CHILLING REVELATION: Tucker Carlson Reveals Dems NEXT PLAN to STOP Trump!
70.9K27 -
 6:51
6:51
Colion Noir
6 hours agoI have Something To Say To Gun Owners
42.9K16 -
 1:18:24
1:18:24
Glenn Greenwald
10 hours agoLiberals Encourage Family & Friends To Separate Over Political Disputes; Segment Debut Of System Pupdate: Profiles Of Rescued Dogs | SYSTEM UPDATE #373
102K153 -
 1:24:53
1:24:53
Flyover Conservatives
1 day agoMarketing Madness or Manipulation? The War on Western Identity - Alex Newman; Economic Update - Dr. Kirk Elliott | FOC Show
39K5 -
 1:15:05
1:15:05
PMG
1 day ago $6.96 earned"Big Pharma EXPOSED: The HIDDEN Cures They Tried to Bury"
32.4K6 -
 3:26:12
3:26:12
Tundra Gaming Live
7 hours ago $2.14 earnedThe Worlds Okayest War Thunder Stream
29.1K1