Premium Only Content
Laboratory Project: Taylor Polynomials: Question 2: Approximation Accuracy
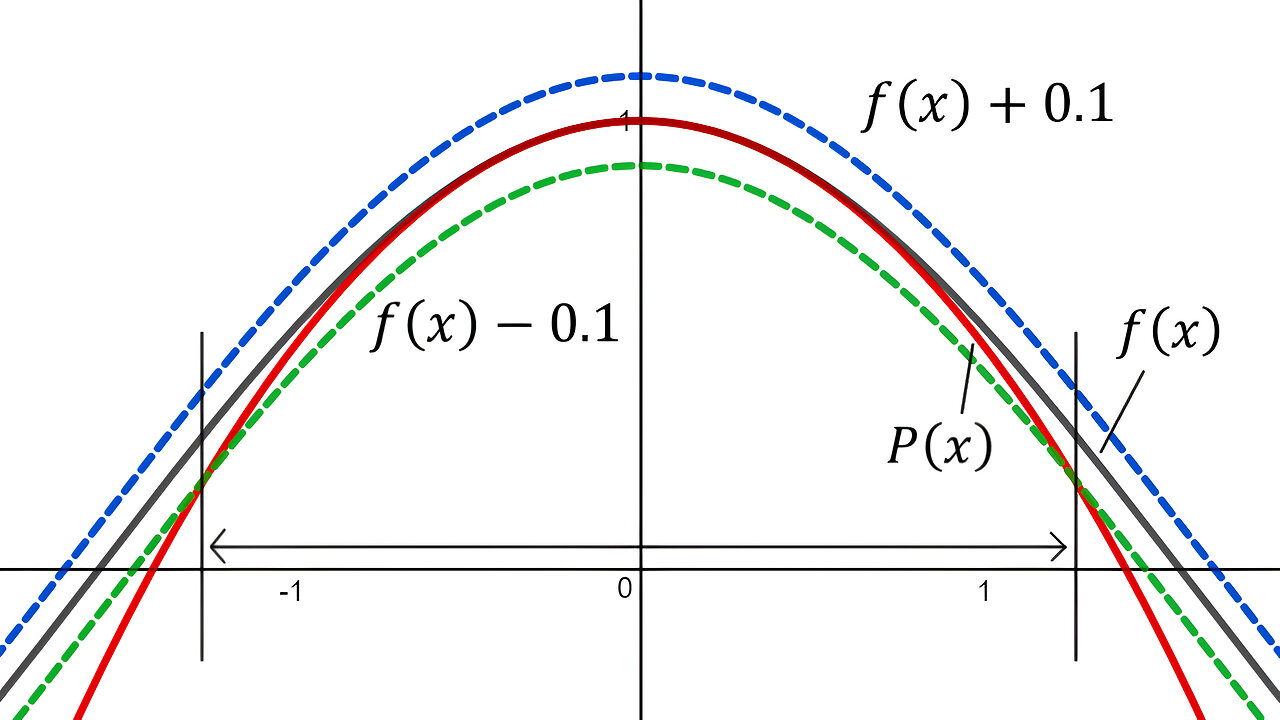
In this video I go over Question 2 of the Laboratory Project: Taylor Polynomials and this time look at determining the accuracy of the quadratic approximation determined in Question 1. Recall from Question 1 that I showed that the quadratic or parabola approximation P(x) = 1 – (x^2)/2 was much more accurate in approximating f(x) = cos(x) than a simple Linear Approximation. In this video I look at that determining the values of x in which the given accuracy is within 0.1. In other words the absolute value of the difference f(x) – cos(x) is within 0.1. To determine this I first graph the functions P(x), f(x), as well as f(x) + 0.1 and f(x) – 0.1. This allows us to visually see the region in which P(x) is accurate to within 0.1. Zooming into the intersection I show that it is equal to +/- 1.26.
Also shown in this video is a look at a numerical online solver approach to determine a more accurate value for the range. But when dealing with inequalities and numerical calculations it is important to understand that rounding up or rounding down can affect the given inequality, so always keep this in mind! This is a very useful video in understanding the accuracy associated with graphical and numerical approximations, so make sure to watch this video!
Video notes and playlist:
- PDF: https://1drv.ms/b/s!As32ynv0LoaIh44lr-8yFszdUmViLQ
- HIVE: https://peakd.com/mathematics/@mes/laboratory-project-taylor-polynomials-question-2-approximation-accuracy
- Laboratory Projects playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0GPz_diCZTkiVs6Q4mA_KHb
Related Videos:
Laboratory Project: Taylor Polynomials: Question 1: Quadratic Approximation: https://youtu.be/8bpF3vccvEU
Taylor Polynomials - Introduction and Derivation: http://youtu.be/p2EkXwkbflk
Linear Approximation - Introduction and Examples: http://youtu.be/bXEK8bkWTtM
tan(x) = sin(x) = x and cos(x) = 1 near x = 0: Linear Approximation in Physics: http://youtu.be/TPtZIxICa3Q
Differentials Notation in Linear Approximation: http://youtu.be/s0adatWiZg4
Newton's Method of Linear Approximation - Introduction: http://youtu.be/aT4b_5l50RI .
------------------------------------------------------
Become a MES Super Fan! https://www.youtube.com/channel/UCUUBq1GPBvvGNz7dpgO14Ow/join
DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate
SUBSCRIBE via EMAIL: https://mes.fm/subscribe
MES Links: https://mes.fm/links
MES Truth: https://mes.fm/truth
Official Website: https://MES.fm
Hive: https://peakd.com/@mes
Email me: contact@mes.fm
Free Calculators: https://mes.fm/calculators
BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm
Free Online Tools: https://mes.fm/tools
iPhone and Android Apps: https://mes.fm/mobile-apps
-
 59:05
59:05
Math Easy Solutions
16 days ago $0.01 earnedAnimal Diversity: Sponges, Chordates, Vertebrates, Blastulation, Food Chain
1282 -
 1:24:20
1:24:20
Vigilant News Network
23 hours agoJoe Rogan Drops Shocking Election Claim | The Daily Dose
136K123 -
 1:10:18
1:10:18
FamilyFriendlyGaming
22 hours ago $18.14 earnedCat Quest III Episode 2
118K -
 20:07
20:07
DeVory Darkins
1 day ago $20.78 earned"They Talking About Finance!" The View FRUSTRATED by NYC Mayor TRUTH BOMB
86.9K93 -
 1:20:18
1:20:18
Steve-O's Wild Ride! Podcast
2 days ago $11.64 earnedThe Hawk Tuah Girl Is Really Becoming Successful! - Wild Ride #243
65.6K5 -
 1:29:26
1:29:26
Game On!
1 day ago $10.04 earnedJon Jones vs Stipe Miocic Heavyweight Title Fight | UFC 309 Preview
61.6K5 -
 30:26
30:26
The Why Files
7 days agoThe Pascagoula UFO Incident | When Nightmares Come True
90.6K62 -
 1:40:28
1:40:28
Roseanne Barr
2 days ago $70.50 earnedUnredacting Jesus with Billy Phillips | The Roseanne Barr Podcast #74
174K187 -
 55:49
55:49
Stephen Gardner
1 day ago🔥SECRET TRAPS laid for Trump, RFK & ELON | Megyn Kelly worries for Trump's life, CIA vote algorithm.
71.7K146 -
 1:24:47
1:24:47
Kim Iversen
1 day agoMafia Tactics: A Private Equity Firm Forced Her Into An Abortion To Retaliate Against Her Speaking Up.
238K277