Premium Only Content
Slant Asymptote Lines + Special Case: Rational Functions and Long Division
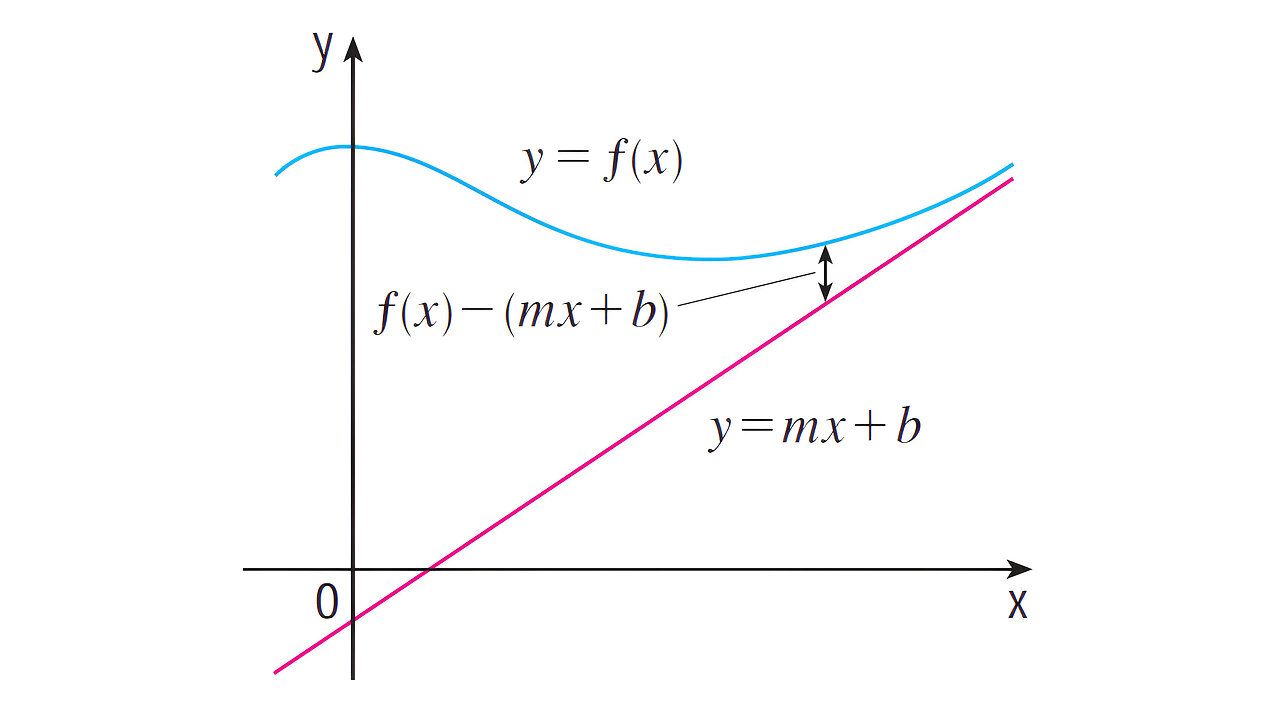
In this video I go over Slant Asymptotes as well as the special case of finding Slant Asymptotes of Rational Functions through Polynomial Long Division. I actually briefly covered Slant asymptotes in my earlier video, so please ignore my statement in the video in which I said I should have covered this a long time ago, nonetheless I didn’t actually prove the special case in my earlier video. A slant asymptote is just that, an asymptote that is slanted, which is to say neither vertical nor horizontal. In other words a slanted asymptote is a linear function, and a function is said to have an slanted asymptote if it approaches the slanted line as x approaches positive or negative infinity. We can write this mathematically as the limit as x approaches infinity of the DIFFERENCE between the function and a linear function is equal to 0; i.e. the function is approaching the same value of the linear function.
The special case for slant asymptotes occurs for Rational Functions in which the degree (or highest power) of the numerator is ONE MORE than the degree of the denominator. Recall that a rational function is a division of two polynomials on the domain that the denominator is not equal to zero. Thus when we use polynomial long division to divide out these two polynomials, I show that we end up with a quotient that is in fact a linear function, i.e. has a degree of 1. And combined with the fact that the remainder has a degree less than the divisor or denominator, as shown by Euclidean Division for Polynomials, then the difference between the function and the linear quotient is simply equal to the remainder divided by the denominator. Now the limit of the latter, as I show in the video, is equal to 0 because the higher power denominator approaches infinity “faster” than the remainder thus obtaining a 1 divided by infinity scenario, i.e. approaches 0. And this proves the special case and the quotient is the linear function which is the slant asymptote.
This is a very detailed video into slant asymptotes, especially the derivation of the special case, so make sure to watch this video!
Video Notes and Playlist:
- PDF notes: https://1drv.ms/b/s!As32ynv0LoaIh5AAP5jQxzqGnaj_ww
- HIVE notes: https://peakd.com/mathematics/@mes/slant-asymptote-lines-special-case-rational-functions-and-long-division
- Slant Asymptotes playlist: https://www.youtube.com/playlist?list=PLA196AE9726C3DC6A
Related Videos:
Euclidean Division of Polynomials: Theorem and Proof: https://youtu.be/ONxn17okl5c
Polynomial Long Division - In depth Look on why it works!: http://youtu.be/E1H584xJS_Y
Rational and Algebraic Functions - A Brief Explanation: http://youtu.be/4mvNTeXEW-k
Slant Asymptotes - Guidelines to Curve Sketching: http://youtu.be/1pk9ZPPyXGo
Rational and Algebraic Functions - A Brief Explanation: http://youtu.be/4mvNTeXEW-k
Law of Exponents a^(x-y) = (a^x)/(a^y): http://youtu.be/djwpuNtmYJY .
------------------------------------------------------
Become a MES Super Fan! https://www.youtube.com/channel/UCUUBq1GPBvvGNz7dpgO14Ow/join
DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate
SUBSCRIBE via EMAIL: https://mes.fm/subscribe
MES Links: https://mes.fm/links
MES Truth: https://mes.fm/truth
Official Website: https://MES.fm
Hive: https://peakd.com/@mes
Email me: contact@mes.fm
Free Calculators: https://mes.fm/calculators
BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm
Free Online Tools: https://mes.fm/tools
iPhone and Android Apps: https://mes.fm/mobile-apps
-
 3:32:23
3:32:23
Math Easy Solutions
12 days ago $0.09 earnedMES Livestream 67: MH370 Teleportation Video Creator Joins the Show!
5652 -
 29:53
29:53
MYLUNCHBREAK CHANNEL PAGE
1 day agoUnder The Necropolis - Pt 1
88.2K43 -
 2:00:10
2:00:10
Bare Knuckle Fighting Championship
3 days agoCountdown to BKFC on DAZN HOLLYWOOD & FREE LIVE FIGHTS!
42.6K3 -
 2:53:01
2:53:01
Jewels Jones Live ®
1 day agoA MAGA-NIFICENT YEAR | A Political Rendezvous - Ep. 103
100K24 -
 29:54
29:54
Michael Franzese
12 hours agoCan Trump accomplish everything he promised? Piers Morgan Article Breakdown
104K49 -
 2:08:19
2:08:19
Tactical Advisor
16 hours agoThe Vault Room Podcast 006 | Farwell 2024 New Plans for 2025
178K11 -
 34:12
34:12
inspirePlay
1 day ago $5.45 earned🏆 The Grid Championship 2024 – Cass Meyer vs. Kelly Rudney | Epic Battle for Long Drive Glory!
80.3K8 -
 17:50
17:50
BlackDiamondGunsandGear
13 hours ago $2.61 earnedTeach Me How to Build an AR-15
54.9K6 -
 9:11
9:11
Space Ice
1 day agoFatman - Greatest Santa Claus Fighting Hitmen Movie Of Mel Gibson's Career - Best Movie Ever
114K47 -
 42:38
42:38
Brewzle
1 day agoI Spent Too Much Money Bourbon Hunting In Kentucky
76.6K12