Premium Only Content
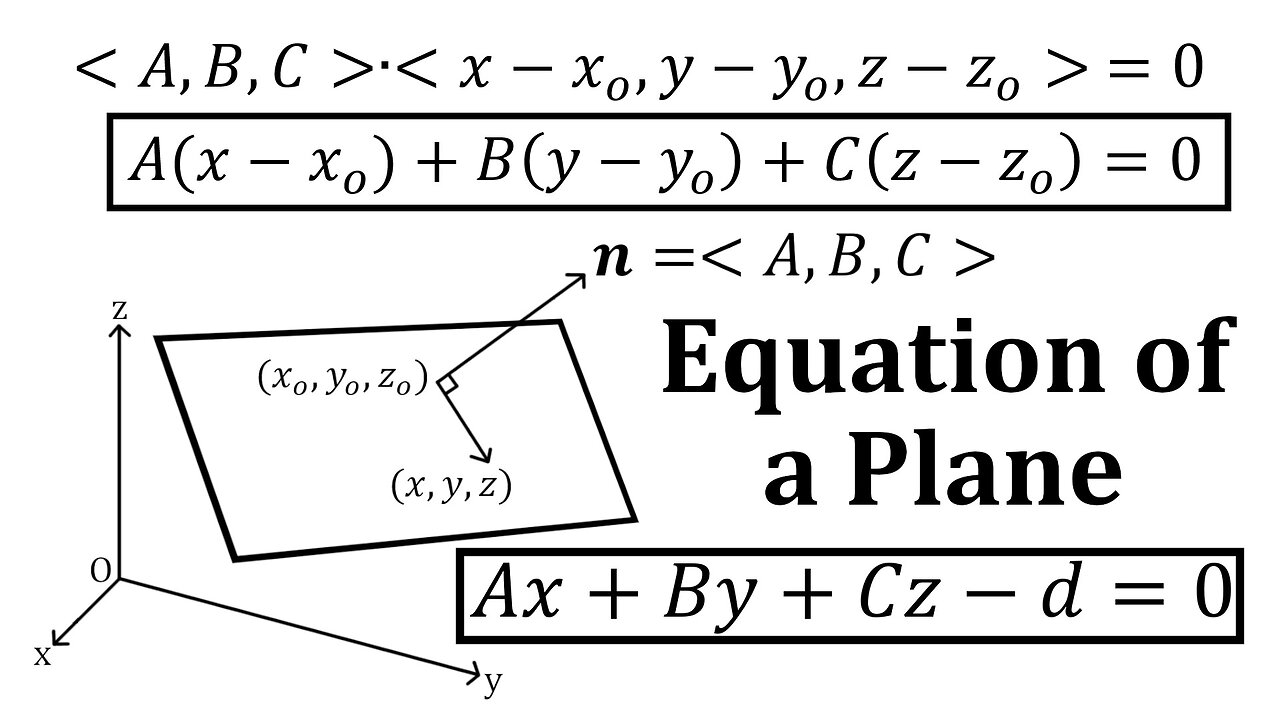
Equation of a Plane: Derivation Using the Dot Product
In this video I go over the equation of a plane and derive it by using the Dot Product. A plane is a flat set of points in 3D. If we draw a vector parallel to it and another vector perpendicular (or normal) to the plane, then the resulting dot product of these 2 vectors must equal 0. This can then be used to derive the equation of a plane. I write the equation in 2 forms, a longer one and a shortened one that replaces the constants with the term "d".
This video was taken from my earlier video listed below:
- Discovery Project: The Geometry of a Tetrahedron: https://youtu.be/yRws7Jk2iHU
- Video notes: https://peakd.com/hive-128780/@mes/discovery-project-geometry-of-a-tetrahedron
- Playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0GoEi9wxl8nTFcfw1ay-_1T
------------------------------------------------------
SUBSCRIBE via EMAIL: https://mes.fm/subscribe
DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate
Like, Subscribe, Favorite, and Comment Below!
Follow us on:
MES Truth: https://mes.fm/truth
Official Website: https://MES.fm
Hive: https://peakd.com/@mes
MORE Links: https://linktr.ee/matheasy
Email me: contact@mes.fm
Free Calculators: https://mes.fm/calculators
BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm
Free Online Tools: https://mes.fm/tools
iPhone and Android Apps: https://mes.fm/mobile-apps
-
 3:13:41
3:13:41
Math Easy Solutions
13 days ago $0.04 earnedMES Livestream 84: Moon Landing Deep Dive
3682 -
 4:19:36
4:19:36
SynthTrax & DJ Cheezus Livestreams
16 hours agoFriday Night Synthwave 80s 90s Electronica and more DJ MIX Livestream THE GREAT EDO WARS OF 2067 Edition
65.3K4 -
 4:45:15
4:45:15
RalliedLIVE
6 hours ago $1.60 earnedWarzone Domination w/ Ral
47.1K -
 1:10:17
1:10:17
Sarah Westall
8 hours agoWorld Leaders Increasingly Display Panic Behavior as Economic Change Accelerates w/ Andy Schectman
72.7K15 -
 59:54
59:54
Motherland Casino
5 hours ago $1.55 earnedScar x Ayanna
27.9K5 -
 41:57
41:57
BonginoReport
10 hours agoProtecting Kids From WOKE Ideology in School (Ep. 35) - Nightly Scroll with Hayley Caronia -04/25/25
118K49 -
 LIVE
LIVE
SpartakusLIVE
8 hours agoFriday Night HYPE w/ #1 All-American Solo NUKE Hero
147 watching -
 1:15:07
1:15:07
Kim Iversen
1 day agoThe Left Is Dead — What And Who Will Rise From the Ashes?
103K79 -
 2:06:17
2:06:17
Joker Effect
5 hours agoYOU DON'T UNDERSTAND FREEDOM OF SPEECH IF THIS MAKES YOU MAD!
14.6K1 -
 1:45:26
1:45:26
vivafrei
12 hours agoSantos Sentenced to 87 MONTHS! Corrupt Judges ARRESTED! Some Canada Stuff & MORE!
144K93