Premium Only Content
Conics in Polar Coordinates: Unified Theorem: Hyperbola Proof
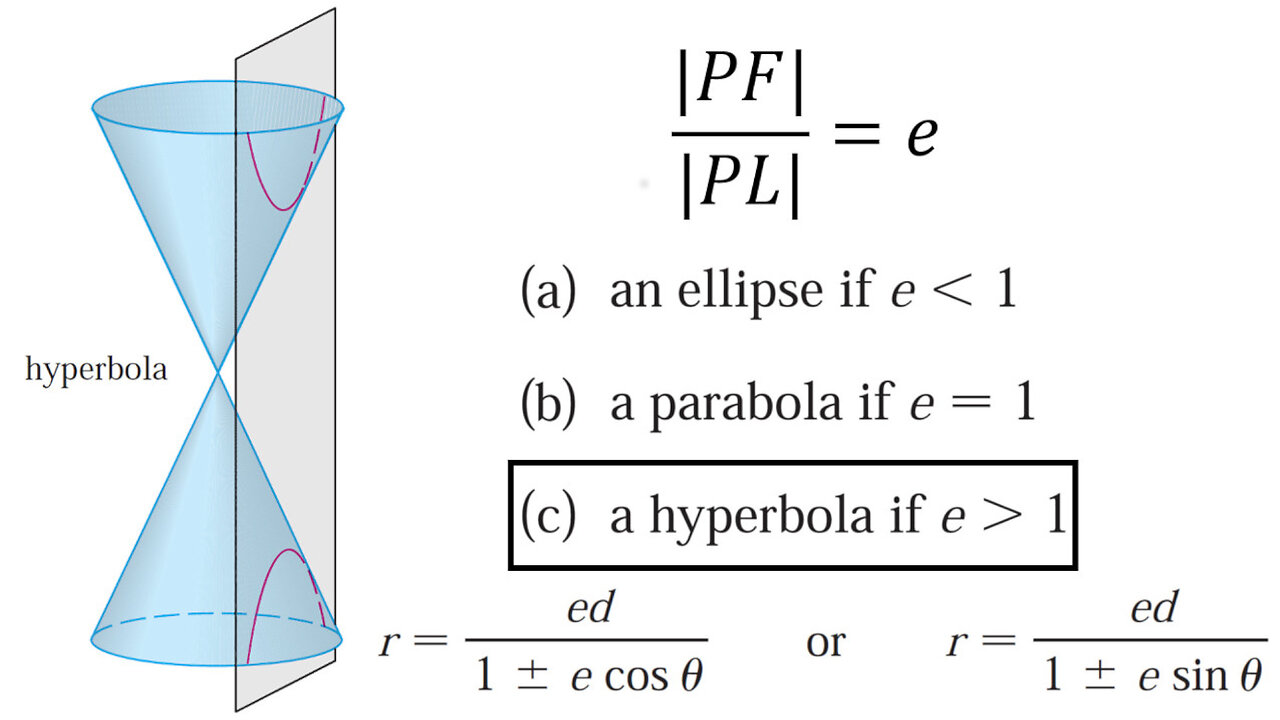
In this video I go over further into the Unified the Theorem for Conics and this time prove it is applicable for hyperbolas. Recall that the theorem states that a conic is formed when the ratio of the distance to the focus divided by the distance to the directrix is a constant e, called the eccentricity. In my earlier videos I proved the case for parabolas (e = 1) and ellipses (e is less than 1), and in this video I prove the case for when e is greater than 1, i.e. for hyperbolas. But to save time I carry off from the proof of ellipses in which I first derived a formula for the conic for the general case of e is not equal to 1. The resulting formula in Cartesian or Rectangular coordinates looks very much like that for ellipses and hyperbolas, but the different values of e decides which conic is described. For the case that e is greater than 1, I show that indeed the unified theorem describes a hyperbola, and in fact it is a shifted horizontally shifted horizontal hyperbola. And just like for the ellipses case, the focus defined by the unified theorem is the exact same as that defined by the conventional theorem, albeit having two foci.
This is a very important video to understand how different theorems can describe the same curve but for better or worse across different coordinate systems. I will be going over some examples in later videos to better illustrate this theorem and its very simple formulation in polar coordinates so stay tuned!
Download the notes in my video: https://1drv.ms/b/s!As32ynv0LoaIh5pCF992AdJKQ8h1Dw
View video notes on the Hive blockchain: https://peakd.com/mathematics/@mes/conics-in-polar-coordinates-unified-theorem-hyperbola-proof
Related Videos:
Conics in Polar Coordinates Playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0H4OJpJ2gslXVLT8mP-SgJP
Conic Sections Playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0FEUsuxP3KS5DRbidSSGBPL
Polar Coordinates Playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0HUFiPLsYw5_Ljd5riOUzjP
Conics in Polar Coordinates: Unified Theorem: Ellipse Proof: https://youtu.be/HRFzk1vyLmg .
------------------------------------------------------
SUBSCRIBE via EMAIL: https://mes.fm/subscribe
DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate
Like, Subscribe, Favorite, and Comment Below!
Follow us on:
MES Truth: https://mes.fm/truth
Official Website: https://MES.fm
Hive: https://peakd.com/@mes
MORE Links: https://linktr.ee/matheasy
Email me: contact@mes.fm
Free Calculators: https://mes.fm/calculators
BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm
Free Online Tools: https://mes.fm/tools
iPhone and Android Apps: https://mes.fm/mobile-apps
-
 2:02:07
2:02:07
Math Easy Solutions
3 days ago $0.01 earnedMES Livestream 74: Revisiting Disinfo Agent Blue Bacon with 9/11 Revisited
1992 -
 LIVE
LIVE
The Rubin Report
49 minutes agoJD Vance Makes Host Go Quiet with This Brutal Warning for These Major Countries
4,154 watching -
 LIVE
LIVE
Steven Crowder
2 hours ago🔴 Why Trump & America Will Dominate the Global Trade War
47,550 watching -
 DVR
DVR
vivafrei
14 hours agoLive with "Bitcoin Jesus" Roger Ver - the Indictment, Law-Fare and the War on Crypto
27.8K5 -
 LIVE
LIVE
Bannons War Room
1 year agoWarRoom Live
32,908 watching -
 LIVE
LIVE
LFA TV
22 hours agoTARIFF TRADE WAR! | LIVE FROM AMERICA 2.3.25 11am
4,378 watching -
 LIVE
LIVE
Caleb Hammer
56 minutes agoProfessional Redditor Treats His Wife Like A Pet | Financial Audit
228 watching -

Rethinking the Dollar
45 minutes agoMonday Morning Check-In | Tit-for-Tat Trade Wars: Why Gold Is Still Winning
-
 56:02
56:02
Randi Hipper
1 hour agoBITCOIN AT CRITICAL LEVELS AS MARKET CRASHES! LATEST PRICE UPDATE HERE
3.99K1 -

Matt Kohrs
10 hours agoMARKET CRASH! Trump's Trade War Bloodbath || The MK Show
24.6K6