Premium Only Content
Ausblick auf das nächste Video ► Logarithmische Verzweigungspunkte mehrwertiger komplexer Funktionen
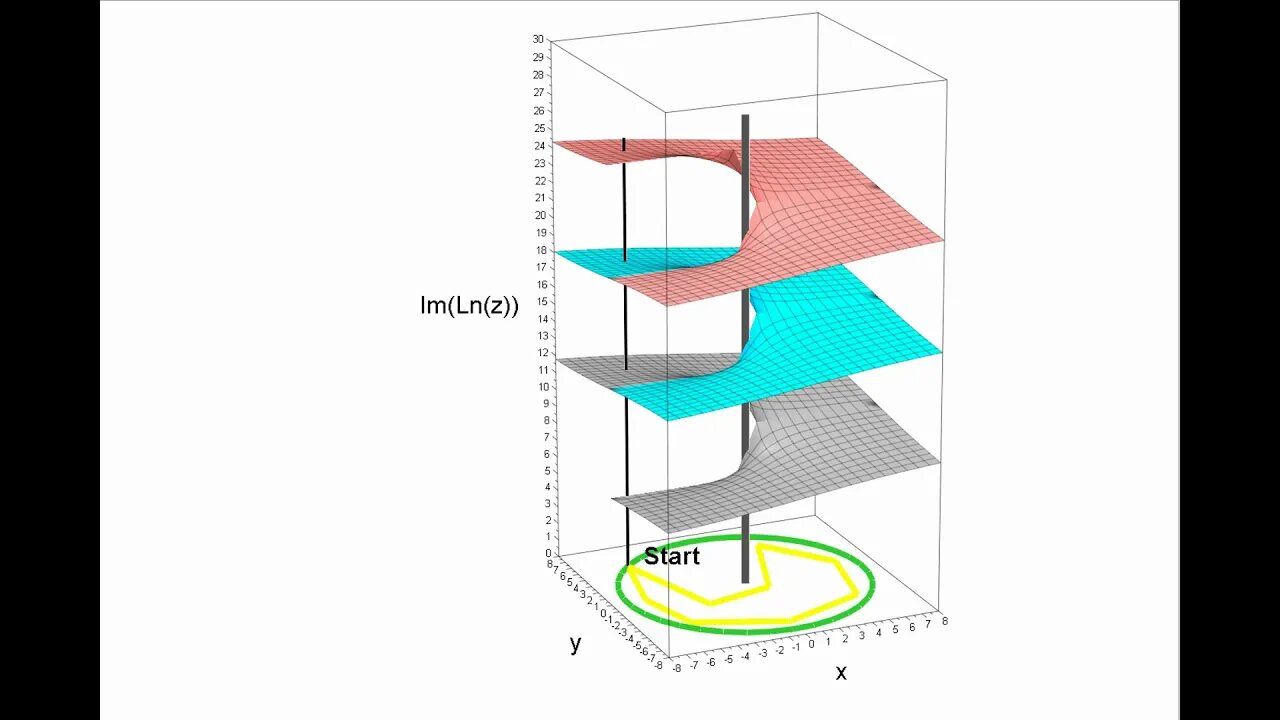
Mehrwertige komplexe Funktionen (hier die komplexe Logarithmusfunktion) haben Verzweigungspunkte (bei der Logarithmusfunktion liegt er bei 0/0). Im Bild sehen wir den Imaginärteil über der z-Ebene aufgetragen.
►Legt man nun in der z-Ebene einen geschlossenen Weg zurück, der den Verzweigungspunkt umrundet (grüner Weg), so ändert sich der Imaginärteil um 2 Pi (pro Umrundung), weil man im neuen Zweig landet.
►Legt man aber einen geschlossenen Weg zurück, der den Verzweigungspunkt NICHT umrundet (gelb), dann ändert sich der zugehörige Imaginärteil nicht.
Dies alles wird in den nächsten Videos erklärt. Dort werden wir auch nicht-logarithmische Verzweigungspunkte anhand Riemannscher Flächen erklären.
Kanalmitgliedschaft:
https://www.youtube.com/channel/UCiT0SUtIWTQZQd1galJ-hpw/join
Linklisten:
Es existieren viele Linklisten im Web, z.B. hier: http://www.mathematik.net
-
 6:57
6:57
Cooking with Gruel
15 hours agoMake Cheese Great Again
7914 -
 5:17
5:17
Mrgunsngear
18 hours ago $1.64 earnedPresident Trump Has Appointed A New ATF Director
4.86K17 -
 38:30
38:30
hickok45
3 hours agoSunday Shoot-a-Round # 269
4761 -
 1:39:55
1:39:55
Squaring The Circle, A Randall Carlson Podcast
22 hours ago#040 Humanity's Expansion Into The Cosmos: A New Age - Squaring The Circle
1.8K3 -
 12:54
12:54
ariellescarcella
12 hours agoYou're NOT Queer, Just Annoying And Boring
61 -
 18:57
18:57
Fit'n Fire
9 hours agoA PDW That Thumps -- Stribog SP45A3 45ACP
751 -
 LIVE
LIVE
Game On!
12 hours ago $0.49 earnedAnother Sunday Without Football...
1,129 watching -
 17:53
17:53
Forrest Galante
14 hours agoHow I Joined a Dangerous Remote Tribe (feat. Nelk Boys)
66.2K12 -
 LIVE
LIVE
Vocalot
1 day agoDay 6! New Here! New Rumble Friends!? 🤙
1,572 watching -
 34:27
34:27
The Connect: With Johnny Mitchell
19 hours ago $14.90 earnedCan He Stop Them? Inside Trumps War On Mexican Drug Cartels & The New Era Of Mexican Organized Crime
41.3K24