Premium Only Content
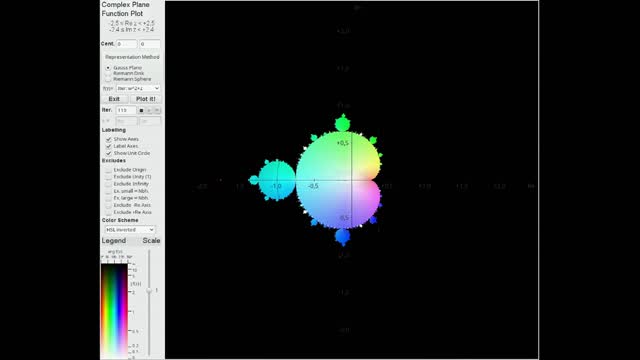
DépêcheMath - Mandelbrot sequence f₀(z) = 0; fₙ₊₁(z) = (fₙ(z))² + z without subtitles
Animated development of the "Mandelbrot" sequence f₀(z) = 0; fₙ₊₁(z) = (fₙ(z))² + z without mathematical subtitles.
Music: Doug Maxwell, Cast of Pods
This animation covers the recursively defined sequence of polynomials f₀(z) = 0; fₙ₊₁(z) = (fₙ(z))² + z which is closely related to the famous Mandelbrot fractal set. Its development is depicted by coloring the points of the complex plane according to the values of fₙ(z). See the legend in the lower left corner for how to translate these colors to complex values or halt this animation at f₁(z) = z which is the identity map and study the correspondence between colors and positions in the complex plane.
Speaking in terms of dynamical systems theory, we discuss this recursion not in the dynamic plane but rather in the parameter plane and study the sequence members as functions of this parameter.
Animation imaging was created using "Complex Plane Viewer" (CPV), a program written by myself for visualizing complex functions, developed within the Lazarus IDE.
-
 DVR
DVR
Robert Gouveia
1 hour agoTrump Goes to SCOTUS! Judge CAVES on DOGE? Fani Willis Not Happy!
6.23K1 -
 20:41
20:41
Stephen Gardner
1 hour ago🔥You Won't BELIEVE What JUST Happened To Don Trump Jr.!!
2.25K36 -
 1:06:40
1:06:40
Donald Trump Jr.
5 hours agoThe Left is Taking one L After Another, Live with Michael Knowles | Triggered Ep. 217
40.6K59 -
 47:17
47:17
Kimberly Guilfoyle
5 hours agoWoke Gets DOGE’d, Live with AJ Rice & Jarrett Stepman | Ep. 197
32.2K28 -
 20:11
20:11
Candace Show Podcast
3 hours agoBecoming Brigitte: Candace Owens x Xavier Poussard | Ep 6
81.6K225 -
 LIVE
LIVE
Dr Disrespect
8 hours ago🔴LIVE - DR DISRESPECT - ELDEN RING DLC - REVENGE
3,006 watching -
 LIVE
LIVE
LFA TV
1 day agoThe End of the Trans-Atlantic Alliance | TRUMPET DAILY 2.17.25 7PM
325 watching -
 LIVE
LIVE
2 MIKES LIVE
4 hours ago2 MIKES LIVE #181 Deep Dive Monday!
136 watching -
 LIVE
LIVE
Quite Frankly
5 hours ago"Low Tide at The Pier: Munich Tears, World Gov Summit, More..." 2/17/25
1,162 watching -
 DVR
DVR
The Based Mother
5 hours agoBOOK BAN LIES. Karen England and the MSM fairy tale that books are being “banned” by fascists
56