Premium Only Content
Topographic VAEs learn Equivariant Capsules (Machine Learning Research Paper Explained)
#tvae #topographic #equivariant
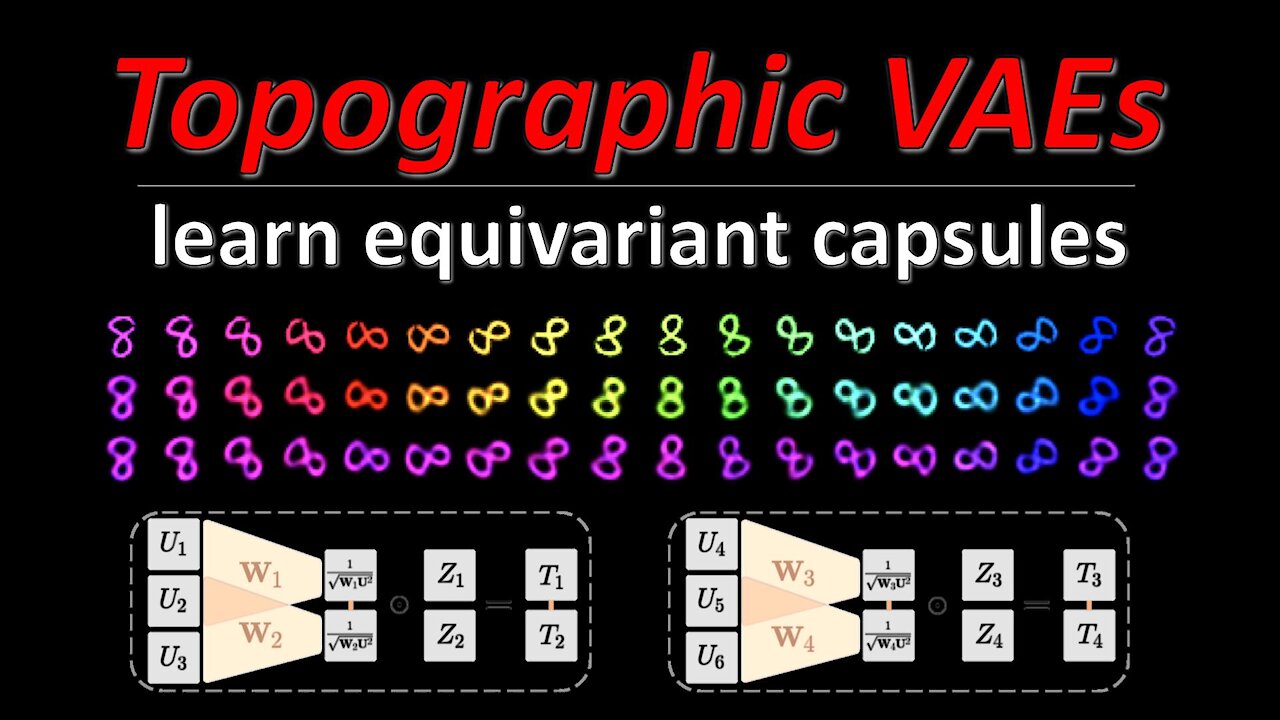
Variational Autoencoders model the latent space as a set of independent Gaussian random variables, which the decoder maps to a data distribution. However, this independence is not always desired, for example when dealing with video sequences, we know that successive frames are heavily correlated. Thus, any latent space dealing with such data should reflect this in its structure. Topographic VAEs are a framework for defining correlation structures among the latent variables and induce equivariance within the resulting model. This paper shows how such correlation structures can be built by correctly arranging higher-level variables, which are themselves independent Gaussians.
OUTLINE:
0:00 - Intro
1:40 - Architecture Overview
6:30 - Comparison to regular VAEs
8:35 - Generative Mechanism Formulation
11:45 - Non-Gaussian Latent Space
17:30 - Topographic Product of Student-t
21:15 - Introducing Temporal Coherence
24:50 - Topographic VAE
27:50 - Experimental Results
31:15 - Conclusion & Comments
Paper: https://arxiv.org/abs/2109.01394
Code: https://github.com/akandykeller/topog...
Abstract:
In this work we seek to bridge the concepts of topographic organization and equivariance in neural networks. To accomplish this, we introduce the Topographic VAE: a novel method for efficiently training deep generative models with topographically organized latent variables. We show that such a model indeed learns to organize its activations according to salient characteristics such as digit class, width, and style on MNIST. Furthermore, through topographic organization over time (i.e. temporal coherence), we demonstrate how predefined latent space transformation operators can be encouraged for observed transformed input sequences -- a primitive form of unsupervised learned equivariance. We demonstrate that this model successfully learns sets of approximately equivariant features (i.e. "capsules") directly from sequences and achieves higher likelihood on correspondingly transforming test sequences. Equivariance is verified quantitatively by measuring the approximate commutativity of the inference network and the sequence transformations. Finally, we demonstrate approximate equivariance to complex transformations, expanding upon the capabilities of existing group equivariant neural networks.
Authors: T. Anderson Keller, Max Welling
Links:
TabNine Code Completion (Referral): http://bit.ly/tabnine-yannick
YouTube: https://www.youtube.com/c/yannickilcher
Twitter: https://twitter.com/ykilcher
Discord: https://discord.gg/4H8xxDF
BitChute: https://www.bitchute.com/channel/yann...
Minds: https://www.minds.com/ykilcher
Parler: https://parler.com/profile/YannicKilcher
LinkedIn: https://www.linkedin.com/in/ykilcher
BiliBili: https://space.bilibili.com/1824646584
If you want to support me, the best thing to do is to share out the content :)
If you want to support me financially (completely optional and voluntary, but a lot of people have asked for this):
SubscribeStar: https://www.subscribestar.com/yannick...
Patreon: https://www.patreon.com/yannickilcher
Bitcoin (BTC): bc1q49lsw3q325tr58ygf8sudx2dqfguclvngvy2cq
Ethereum (ETH): 0x7ad3513E3B8f66799f507Aa7874b1B0eBC7F85e2
Litecoin (LTC): LQW2TRyKYetVC8WjFkhpPhtpbDM4Vw7r9m
Monero (XMR): 4ACL8AGrEo5hAir8A9CeVrW8pEauWvnp1WnSDZxW7tziCDLhZAGsgzhRQABDnFy8yuM9fWJDviJPHKRjV4FWt19CJZN9D4n
-
 44:19
44:19
ykilcher
3 years agoPonderNet: Learning to Ponder (Machine Learning Research Paper Explained)
93 -
 35:29
35:29
ykilcher
3 years agoFastformer: Additive Attention Can Be All You Need (Machine Learning Research Paper Explained)
25 -
 36:36
36:36
ykilcher
3 years ago∞-former: Infinite Memory Transformer (aka Infty-Former / Infinity-Former, Research Paper Explained)
27 -
 1:00:54
1:00:54
The Tom Renz Show
6 hours agoMore Epstein/FBI, a Scary Trade War, & the Dem Echo Chamber
829 -
 40:43
40:43
Kimberly Guilfoyle
7 hours agoDems Double Down on Delusion-Why? Live with Tony Kinnett & Bo French | Ep.202
61.7K30 -
 1:28:42
1:28:42
Redacted News
5 hours agoBREAKING! SOMETHING BIG IS HAPPENING IN EUROPE ALL OUT WAR IS COMING AGAINST RUSSIA, TRUMP FURIOUS
108K262 -
 47:50
47:50
Candace Show Podcast
6 hours agoBREAKING: Judge Makes Statement Regarding Taylor Swift's Text Messages. | Candace Ep 155
94.3K106 -
 DVR
DVR
Josh Pate's College Football Show
3 hours agoCFB’s Most Hated Teams | FSU & Clemson Future | Big Ten Win Totals | Star Rankings Overrated?
5.76K -
 1:33:47
1:33:47
CatfishedOnline
4 hours agoGoing Live With Robert - Weekly Recap
19.4K -
 55:18
55:18
LFA TV
1 day agoEurope’s Sudden Turn Against America | TRUMPET DAILY 3.6.25 7PM
25.5K3