Premium Only Content
This video is only available to Rumble Premium subscribers. Subscribe to
enjoy exclusive content and ad-free viewing.
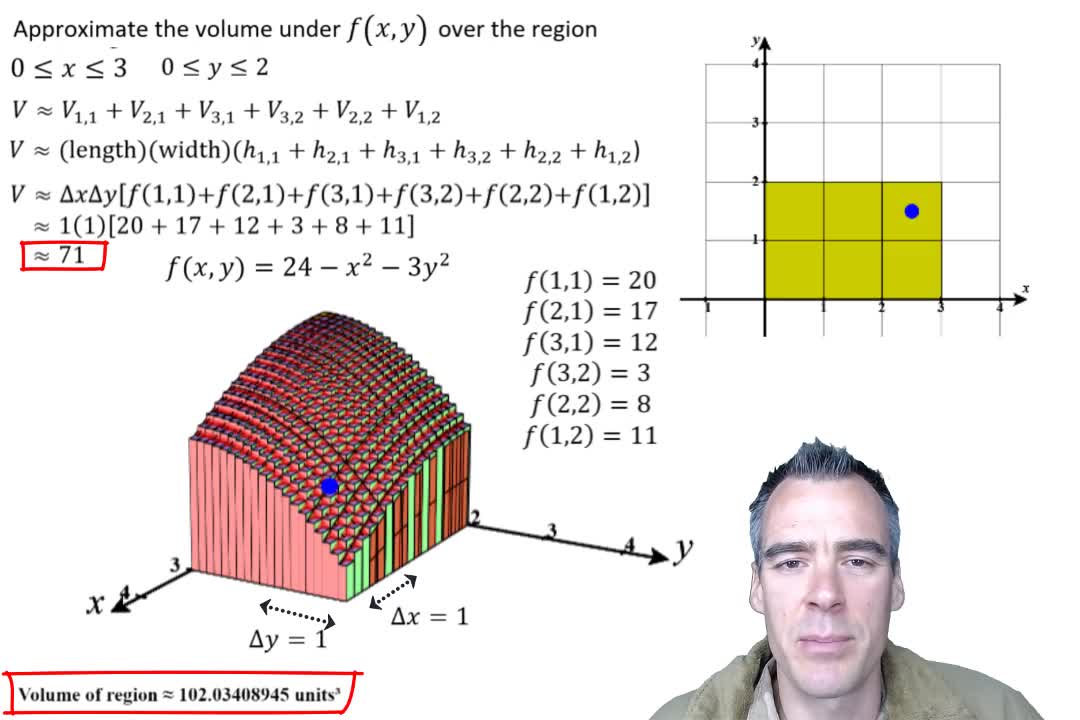
Riemann Sum with 2 Variables
4 years ago
54
We approximate the volume under f(x,y) over the region where 0≤x≤3 and 0≤y≤2.
The volume is approximated in a Riemann Sum of 6 rectangular prisms and visualized in calcplot3D.
The process of taking a difficult problem and cutting it up into smaller easier problems is also discussed, as we find the volume of this solid by cutting it up into 6 rectangular columns. The underestimate is discussed. Each of the six volumes are calculated by find the length, width and height of each prism. The volumes are then summed and the graphic and approximated volume are concurrently shown in CalcPlot3D.
Finally, the next video is introduced within the context of finding a more accurate volume of the solid.
Loading comments...
-
 7:58
7:58
Bits-N-Bytes
4 years agoIntroduction to Python Variables
3571 -
 7:41
7:41
Coding with O Creachmhaoil Studios
4 years agoC++ Tutorial 004: Variables
761 -
 2:08
2:08
smartObjx
4 years agosmartObjx Tutorial - Loading Variables From File
36 -
 0:18
0:18
KTNV
4 years agoCDC adds new social variables to diabeties
45 -
 0:58
0:58
MPIWealthExpert
4 years agoLump Sum Results With MPI™ by Curtis Ray
40 -
 0:25
0:25
eelathrop
4 years agoPlaying with ball
1121 -
 0:10
0:10
Shirt15
4 years agoKid with Fartblaster
1391 -
 0:58
0:58
Middleton123
4 years agoPlaying with a sock
49 -
 50:46
50:46
Esports Awards
17 hours agodGon on Korean League of Legends Dominance, Working the LCS & 2025 Predictions | Origins Podcast #4
10.6K2 -
 12:48
12:48
T-SPLY
16 hours agoDemocrats Keep Digging Their Own Hole Over El Salvadorian Prisoners
34.4K66