Premium Only Content
GREATEST COMMON DIVIDER: APPLICATION EXERCISES
The greatest common factor (GCD) is the largest integer that exactly divides two or more integers. It is also known as the "greatest common factor" or "greatest common divisor."
formal definition
The GCD of two integers a and b is the largest integer that exactly divides a and b.
MCD Properties
1. _Uniqueness_: The GCF of two integers is unique.
2. _Divisibility_: The GCD of two integers divides both numbers exactly.
3. _Maximum_: The GCD is the largest integer that exactly divides both numbers.
4. _Associativity_: The GCF of three integers a, b and c is equal to the GCD of the GCF of a and b, and c.
Methods to find the GCD
1. _Factorization method_: Factor the integers into their prime factors and find the product of the common factors.
2. _Euclid's Method_: Use Euclid's algorithm to find the GCF of two integers.
3. _Subtraction method_: Subtract the smallest number from the largest number until you obtain a remainder of 0. The last remainder other than 0 is the GCF.
Examples
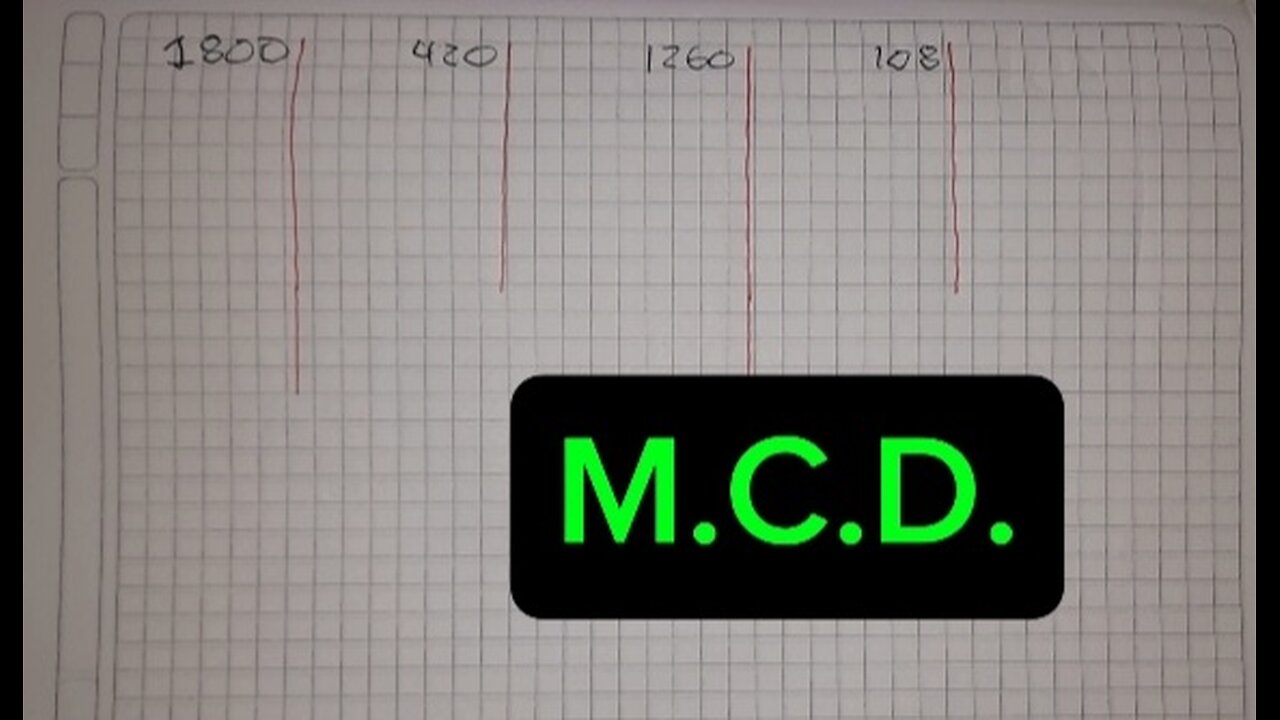
1. Find the GCD of 12 and 18:
- Factorization: 12 = 2^2 × 3, 18 = 2 × 3^2
- GCD: 2 × 3 = 6
1. Find the GCF of 24 and 30:
- Factorization: 24 = 2^3 × 3, 30 = 2 × 3 × 5
- GCD: 2 × 3 = 6
MCD Applications
1. _Number theory_: The GCF is used in number theory to study the properties of integers.
2. _Algebra_: The GCD is used in algebra to find the greatest common divisor of two polynomials.
3. _CRYPTOGRAPHY_: The MCD is used in cryptography to develop encryption and decryption algorithms.
4. _Computer Science_: MCD is used in computer science to develop data processing algorithms.
-
 LIVE
LIVE
Nobodies Gaming
5 hours ago $3.67 earnedNobodies : Rumble Gaming MARVEL RIVALS
1,037 watching -
 24:08
24:08
MYLUNCHBREAK CHANNEL PAGE
1 day agoUnder The Necropolis - Pt 4
51.4K19 -
 19:52
19:52
Adam Does Movies
2 hours ago $0.12 earnedEmilia Pérez Movie Review - It's Uniquely Awful
2.34K -
 20:07
20:07
BlackDiamondGunsandGear
8 hours agoSPRINGFIELD ECHELON COMPACT / NOT GOOD
21.1K1 -
 LIVE
LIVE
Right Side Broadcasting Network
1 day agoLIVE REPLAY: President Donald J. Trump Holds His First Rally After Inauguration in Las Vegas - 1/25/25
5,364 watching -
 2:55:24
2:55:24
Jewels Jones Live ®
1 day agoWEEK ONE IN REVIEW | A Political Rendezvous - Ep. 107
74.4K34 -
 1:33:29
1:33:29
Michael Franzese
1 day agoTrump Wastes No Time: Breaking Down Trump’s First Week Executive Orders | LIVE
107K86 -
 1:26:44
1:26:44
Tactical Advisor
11 hours agoTrump Starting Strong/Shot Show Recap | Vault Room Live Stream 015
70.5K8 -
 10:18
10:18
MrBigKid
7 hours ago $0.35 earnedInsanely Compact Hunting Tripod you HAVEN'T heard of... Revolve
37.2K2 -
 20:29
20:29
marcushouse
14 hours ago $0.44 earnedUnleashing the Power of SpaceX's Starship: Why is it a Big Deal!?
74.2K9