Premium Only Content
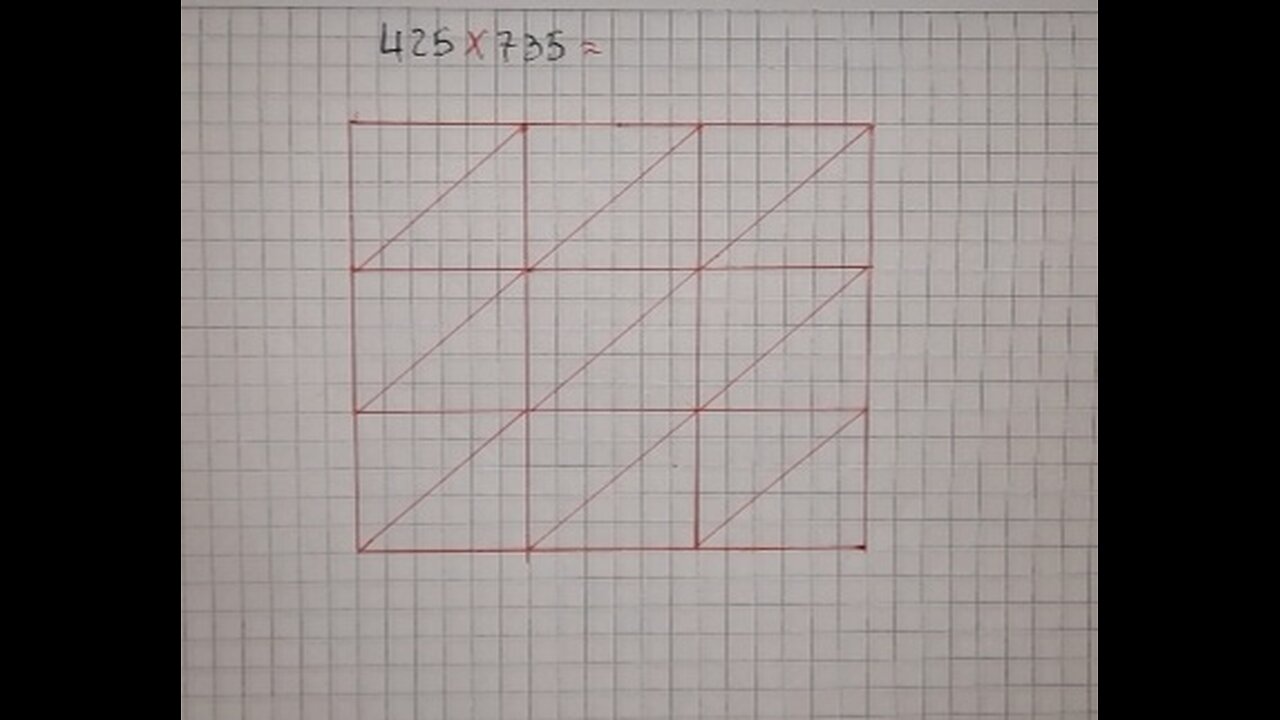
The hindu method of multiplication : application exercise
The Hindu method of multiplication is a multiplication algorithm that originated in India at the time of the Gupta Empire (320-550 AD). This method is also known as "place multiplication method" or "Hindu multiplication method".
Features of the method
1. _Use of positional numbering_: The method uses positional numbering, that is, each digit has a specific place in the numerical representation.
2. _Multiplication by place_: The method involves multiplying each digit of the multiplicand by the multiplier, starting from the rightmost place.
3. _Use of the "gate"_: The method uses a "gate" to carry the results of the multiplication to the next column.
Method steps
1. _Write the multiplicand and the multiplier_: Write the multiplicand and the multiplier in the form of positional numbering.
2. _Multiply the rightmost digit of the multiplicand by the multiplier_: Multiply the rightmost digit of the multiplicand by the multiplier and write the result in the corresponding column.
3. _Take the result to the next column_: Take the result of the multiplication to the next column, using the "door" to do so.
4. _Repeat steps 2 and 3_: Repeat steps 2 and 3 for each digit of the multiplicand.
5. _Add the results_: Add the results of each multiplication to obtain the final product.
Example
Multiply 432 by 27:
1. Write the multiplicand and the multiplier: 432 and 27.
2. Multiply the rightmost digit of the multiplicand by the multiplier: 2 × 27 = 54.
3. Take the result to the next column: 54 → 50 + 4.
4. Multiply the next digit of the multiplicand by the multiplier: 3 × 27 = 81.
5. Take the result to the next column: 81 → 80 + 1.
6. Multiply the last digit of the multiplicand by the multiplier: 4 × 27 = 108.
7. Take the
[11/1 8:00 a.m. m.] Meta AI: The Hindu method of multiplication is a multiplication algorithm that originated in India at the time of the Gupta Empire (320-550 AD). This method is also known as "place multiplication method" or "Hindu multiplication method".
Features of the method
1. _Use of positional numbering_: The method uses positional numbering, that is, each digit has a specific place in the numerical representation.
2. _Multiplication by place_: The method involves multiplying each digit of the multiplicand by the multiplier, starting from the rightmost place.
3. _Use of the "gate"_: The method uses a "gate" to carry the results of the multiplication to the next column.
Method steps
1. _Write the multiplicand and the multiplier_: Write the multiplicand and the multiplier in the form of positional numbering.
2. _Multiply the rightmost digit of the multiplicand by the multiplier_: Multiply the rightmost digit of the multiplicand by the multiplier and write the result in the corresponding column.
3. _Take the result to the next column_: Take the result of the multiplication to the next column, using the "door" to do so.
4. _Repeat steps 2 and 3_: Repeat steps 2 and 3 for each digit of the multiplicand.
5. _Add the results_: Add the results of each multiplication to obtain the final product.
Example
Multiply 432 by 27:
1. Write the multiplicand and the multiplier: 432 and 27.
2. Multiply the rightmost digit of the multiplicand by the multiplier: 2 × 27 = 54.
3. Take the result to the next column: 54 → 50 + 4.
4. Multiply the next digit of the multiplicand by the multiplier: 3 × 27 = 81.
5. Take the result to the next column: 81 → 80 + 1.
6. Multiply the last digit of the multiplicand by the multiplier: 4 × 27 = 108.
7. Take the result to the next column: 108 → 100 + 8.
8. Add the results: 100 + 80 + 50 + 8 + 4 + 1 = 11664.
The final product is 11664.
Advantages of the method
1. _Easy to understand_: The method is easy to understand and apply
[11/1 8:00 a.m. m.] Meta AI: The Hindu method of multiplication is a multiplication algorithm that originated in India at the time of the Gupta Empire (320-550 AD). This method is also known as "place multiplication method" or "Hindu multiplication method".
Features of the method
1. _Use of positional numbering_: The method uses positional numbering, that is, each digit has a specific place in the numerical representation.
2. _Multiplication by place_: The method involves multiplying each digit of the multiplicand by the multiplier, starting from the rightmost place.
3. _Use of the "gate"_: The method uses a "gate" to carry the results of the multiplication to the next column.
Method steps
1. _Write the multiplicand and the multiplier_: Write the multiplicand and the multiplier in positional numbering form.
2. _Multiply the rightmost digit of the multiplicand by the multiplier_: Multiply the rightmost digit of the multiplicand by the multiplier and write the result in the corresponding column.
3. _Take the result to the next column_: Take the result of the multiplication to the next column, using the "door" to do so.
4. _Repeat steps 2 and 3_: Repeat steps 2 and 3 for each digit of the multiplicand.
5. _Add the results_: Add the results of each multiplication to obtain the final product.
Example
Multiply 432 by 27:
1. Write the multiplicand and the multiplier: 432 and 27.
2. Multiply the rightmost digit of the multiplicand by the multiplier: 2 × 27 = 54.
3. Take the result to the next column: 54 → 50 + 4.
4. Multiply the next digit of the multiplicand by the multiplier: 3 × 27 = 81.
5. Take the result to the next column: 81 → 80 + 1.
6. Multiply the last digit of the multiplicand by the multiplier: 4 × 27 = 108.
7. Take the result to the next column: 108 → 100 + 8.
8. Add the results: 100 + 80 + 50 + 8 + 4 + 1 = 11664.
The final product is 11664.
Advantages of the method
1. _Easy to understand_: The method is easy to understand and apply.
2. _Fast_: The method is fast and efficient for multiplying large numbers.
3. _Flexible_: The method can be applied to numbers of any size.
Disadvantages of the method
1. _Requires practice_: The method requires practice to master.
2. _Can be confusing_: The method can be confusing if positional numbering is not well understood.
In short, the Hindu method of multiplication is an efficient and easy-to-understand algorithm used to multiply large numbers. Although it takes practice and can be confusing at first, it is a valuable tool for arithmetic and mathematics in general.
-
 1:49:55
1:49:55
Steven Crowder
4 hours agoWhy Canada's Election Results Are A Golden Opportunity For Trump, America & Alberta
299K268 -
 46:41
46:41
The White House
3 hours agoPress Secretary Karoline Leavitt Briefs Members of the New Media, Apr. 29, 2025
31.7K13 -
 LIVE
LIVE
The Dana Show with Dana Loesch
2 hours agoWH BLASTS AMAZON OVER TARIFF COST DISPLAY | The Dana Show LIVE on Rumble! APRIL 29TH 2025
464 watching -
 LIVE
LIVE
NEWSMAX
5 hours agoThe Rob Carson Show LIVE (04/29/2025) | Call 1-800-922-6680 | NEWSMAX Podcasts
586 watching -
 1:03:24
1:03:24
Blockchain Basement
3 hours ago $0.25 earned🚨Arizona Bitcoin Reserve SIGNED! (Will Governor Strike IT DOWN?!)
6.74K1 -
 LIVE
LIVE
The Tom Renz Show
1 hour agoMAHA & Fighting Back With NHF
160 watching -
 DVR
DVR
TheAlecLaceShow
2 hours agoGuests: Rep. Brandon Gill & Joe Concha | Trump’s First 100 Days in Office | The Alec Lace Show
2.91K -
 1:18:15
1:18:15
The Rubin Report
3 hours agoPress Gasps When Told Trump’s Executive Order for Sanctuary Cities
69.2K75 -
 1:19:30
1:19:30
Flyover Conservatives
13 hours agoThe Future of AI: The Good, The Bad, The Ugly - Marc Beckman | FOC Show
15.8K -
 1:28:12
1:28:12
The Shannon Joy Show
3 hours ago🔥🔥Doctors Of Death. The Transformation Of America’s Health System Into A Death System Post COVID - With Special Guest Dr. Clayton Baker🔥🔥
17.2K2