Premium Only Content
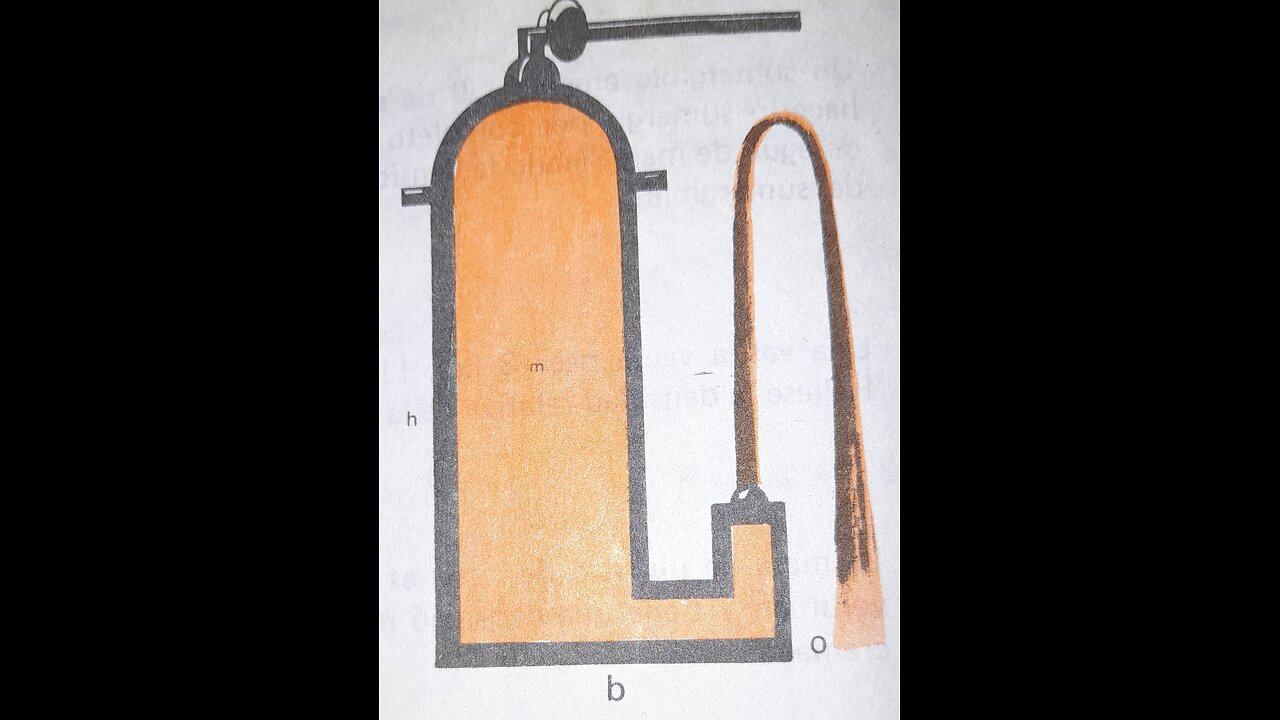
Proofs of Torricelli's theorem: Application exercise
Torricelli's Theorem, also known as the Escape Velocity Theorem, is a fundamental principle in fluid mechanics. It is named after the Italian scientist Evangelista Torricelli.
Theorem Statement
The theorem states that the escape velocity of a fluid through an orifice in a container is equal to the velocity the fluid would have if it fell freely from the surface of the fluid to the level of the orifice.
mathematical formula
v = √(2gh)
where:
1. v is the escape velocity of the fluid
2. g is the acceleration of gravity (approximately 9.81 m/s²)
3. h is the height of the fluid above the orifice
Demonstration
The proof is based on the conservation of energy:
1. *Potential energy on the surface*: mgh
2. *Kinetic energy in the hole*: (1/2)mv²
Equalizing both energies:
mgh = (1/2)mv²
Solving for v:
v = √(2gh)
Applications
1. Design of irrigation systems
2. Calculation of flow in pipes
3. Study of erosion
4. Hydraulic engineering
5. Fluid physics
Examples
1. A hole in a container of water 2 meters high has an escape velocity of √(2_9.81_2) ≈ 4.43 m/s.
2. A faucet with a diameter of 1 cm and a height of 5 meters has an escape velocity of √(2_9.81_5) ≈ 9.9 m/s.
-
 LIVE
LIVE
Man in America
12 hours ago🚨 Chlorine Dioxide: Banned, Censored & Feared by Big Pharma w/ Jonathan Otto
1,853 watching -
 9:21
9:21
Colion Noir
2 hours agoMan Robbed Carrying Gun In Back Pocket, Then Shot Trying To Get It Back
8.43K6 -
 LIVE
LIVE
DLDAfterDark
1 hour agoAnderson American Big Bore pistol Contest!
304 watching -
 LIVE
LIVE
Flyover Conservatives
21 hours agoBiohacking Your Health: The Future of Medicine & Longevity - Part 2 - Deep Dive: Drs. Mark and Michele Sherwood | FOC Show
980 watching -
 LIVE
LIVE
AlaskanBallistics
1 hour ago $0.01 earnedI Love This Gun PodCast #7
120 watching -
 1:04:49
1:04:49
Glenn Greenwald
5 hours agoHow is Trump's Fixation on Taking Over Gaza "America First"?; Netanyahu Never Intended to Carry Through on Ceasefire Deal | SYSTEM UPDATE #405
63.1K79 -
 1:00:06
1:00:06
Rumble Rundown
13 hours agoThe Rumble Rundown: Rumble Studio and Creator Program
68.7K33 -
 14:20
14:20
Timcast
6 hours agoTim Pool HAS JOINED Rumble Premium, HUGE ANNOUNCEMENT, Timcast Exclusive Content Is MOVING
137K272 -
 DVR
DVR
Slightly Offensive
4 hours ago $0.78 earnedELITES Go DEFCON3 on Kanye West, Cancel Culture 2.0 BEGINS! | Nightly Offensive
49.7K6 -
 58:56
58:56
The StoneZONE with Roger Stone
3 hours agoWhy Obama and the Democrats Fear the Blagojevich Pardon | The StoneZONE w/ Roger Stone
40.6K5