Premium Only Content
2563. Count the Number of Fair Pairs
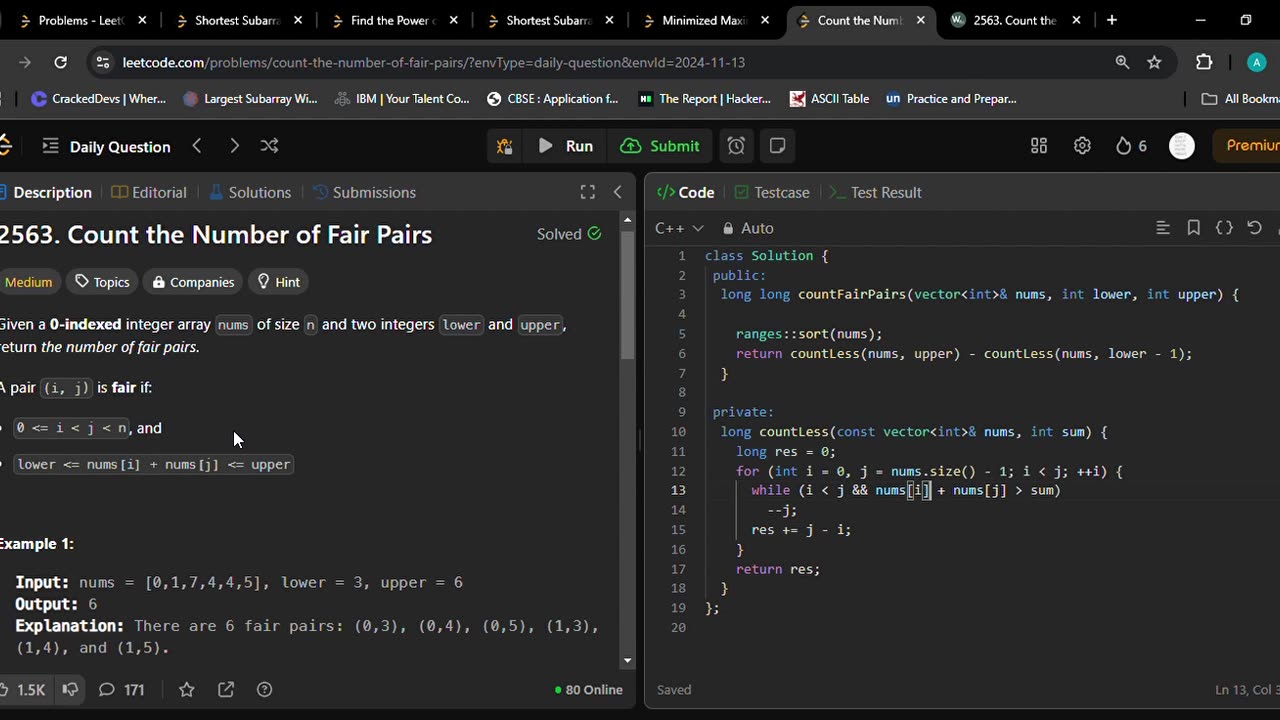
Given a 0-indexed integer array nums of size n and two integers lower and upper, return the number of fair pairs.
A pair (i, j) is fair if:
0 <= i < j < n, and
lower <= nums[i] + nums[j] <= upper
Example 1:
Input: nums = [0,1,7,4,4,5], lower = 3, upper = 6
Output: 6
Explanation: There are 6 fair pairs: (0,3), (0,4), (0,5), (1,3), (1,4), and (1,5).
Example 2:
Input: nums = [1,7,9,2,5], lower = 11, upper = 11
Output: 1
Explanation: There is a single fair pair: (2,3).
Constraints:
1 <= nums.length <= 105
nums.length == n
-109 <= nums[i] <= 109
-109 <= lower <= upper <= 109
class Solution {
public:
long long lower_bound(vector<int>& nums, int low, int high, int element) {
while (low <= high) {
int mid = low + ((high - low) / 2);
if (nums[mid] >= element) {
high = mid - 1;
} else
low = mid + 1;
}
return low;
}
long long countFairPairs(vector<int>& nums, int lower, int upper) {
sort(nums.begin(), nums.end());
long long ans = 0;
for (int i = 0; i < nums.size(); i++) {
// Assume we have picked nums[i] as the first pair element.
// `low` indicates the number of possible pairs with sum < lower.
int low =
lower_bound(nums, i + 1, nums.size() - 1, lower - nums[i]);
// `high` indicates the number of possible pairs with sum <= upper.
int high =
lower_bound(nums, i + 1, nums.size() - 1, upper - nums[i] + 1);
// Their difference gives the number of elements with sum in the
// given range.
ans += 1LL * (high - low);
}
return ans;
}
};
-
 1:56:17
1:56:17
Badlands Media
13 hours agoBaseless Conspiracies Ep. 127: The Satanic Fed Op Behind 764, Pedo Networks & Psychological Warfare with Special Guest, BK
60.2K30 -
 1:05:32
1:05:32
Donald Trump Jr.
12 hours agoNews Not Noise, Live with Power the Future's Daniel Turner | TRIGGERED Ep.231
172K82 -
 28:01
28:01
Side Scrollers Podcast
5 hours agoNEW SERIES! Smash JT Has a Full-On Meltdown | Nerd Duel ft. Lady Desiree & You, Me & The Movies
28.1K2 -
 2:13:28
2:13:28
I_Came_With_Fire_Podcast
7 hours agoMEAD & MENTAL HEALTH WITH I CAME WITH FIRE AND VOC!!!
38K4 -
 1:10:04
1:10:04
John Crump Live
4 hours ago $2.59 earnedYes I talked To The ATF
30.7K3 -
 6:01:28
6:01:28
Amish Zaku
7 hours agoVerDanceKey Warzone - Birthday Fun
33.1K5 -
 LIVE
LIVE
NeoX5
4 hours agoKhazan: The Road Less Taken | Part 5-2 | Rumble Studio | Rumble Gaming
265 watching -
 LIVE
LIVE
TwinGatz
10 hours ago🔴LIVE - He Is Doing His Best | ARMA Reforger
557 watching -
 54:40
54:40
LFA TV
14 hours agoSee God in the Trade War | TRUMPET DAILY 4.7.25 7PM
55.5K12 -
 1:18:30
1:18:30
Sarah Westall
7 hours agoNew Study: EMFs Literally Put You into a Brainwave Cage; Reclaiming your Mind w/ Ian & Philipp
71.3K20