Premium Only Content
The special case of Miquel's theorem when points are collinear | plane geometry | intermediate level
Episode 121.
The special case of Miquel's theorem when points are collinear | plane geometry | intermediate level.
The special case of Miquel's theorem when the points are collinear | plane geometry | intermediate level.
Branch of mathematics: plane geometry.
Difficulty level: intermediate.
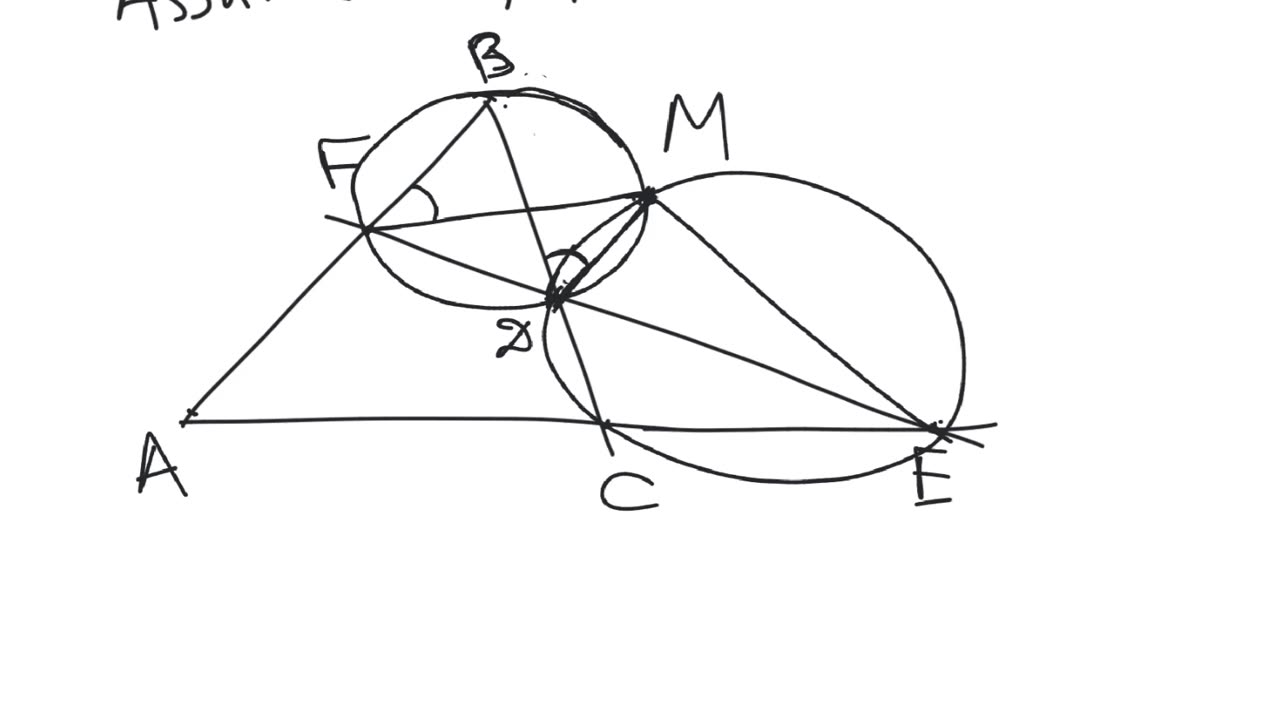
Miquel's theorem. Let $ABC$ be a triangle. Let $D$, $E$, $F$ be arbitrary points on the lines containing the sides $BC$, $CA$, $AB$ of the triangle $ABC$. Then the circumcircles of the triangles $AEF$, $BFD$, $CDE$ intersect at a single point $M$, which is called the Miquel's point.
Special case. The Miquel's point $M$ lies on the circumcircle of the triangle $ABC$ if and only if the points $D$, $E$, $F$ are collinear.
Mathematics. Geometry. Plane geometry.
#Mathematics #Geometry #PlaneGeometry
The same video on YouTube:
https://youtu.be/GOqDf2rtswQ
The same video on Telegram:
https://t.me/mathematical_bunker/146
-
 56:45
56:45
VSiNLive
7 hours ago $5.09 earnedFollow the Money with Mitch Moss & Pauly Howard | Hour 1
73.6K2 -
 52:44
52:44
Candace Show Podcast
7 hours agoMy Conversation with Only Fans Model Lilly Phillips | Candace Ep 122
93.5K323 -
 LIVE
LIVE
tacetmort3m
8 hours ago🔴 LIVE - RELIC HUNTING CONTINUES - INDIANA JONES AND THE GREAT CIRCLE - PART 5
216 watching -
 26:52
26:52
Silver Dragons
6 hours agoCoin Appraisal GONE WRONG - Can I Finally Fool the Coin Experts?
35.6K2 -
 6:49:16
6:49:16
StoneMountain64
10 hours agoNew PISTOL meta is here?
34.9K1 -
 20:58
20:58
Goose Pimples
12 hours ago7 Ghost Videos SO SCARY You’ll Want a Priest on Speed Dial
21K3 -
 2:24:59
2:24:59
The Nerd Realm
10 hours ago $2.80 earnedHollow Knight Voidheart Edition #09 | Nerd Realm Playthrough
36.9K2 -
 1:21:14
1:21:14
Awaken With JP
12 hours agoDrones are for Dummies - LIES Ep 70
120K58 -
 1:47:29
1:47:29
vivafrei
10 hours agoJustin Trudeau Regime ON THE VERGE OF COLLAPSE! And Some More Fun Law Stuffs! Viva Frei
93.1K81 -
 1:52:22
1:52:22
The Quartering
10 hours agoNew Brett Cooper Drama, Madison Feminist Manifesto, Sydney Sweeney Outrage & More
93.1K37