Premium Only Content
The special case of Miquel's theorem when points are collinear | plane geometry | intermediate level
Episode 121.
The special case of Miquel's theorem when points are collinear | plane geometry | intermediate level.
The special case of Miquel's theorem when the points are collinear | plane geometry | intermediate level.
Branch of mathematics: plane geometry.
Difficulty level: intermediate.
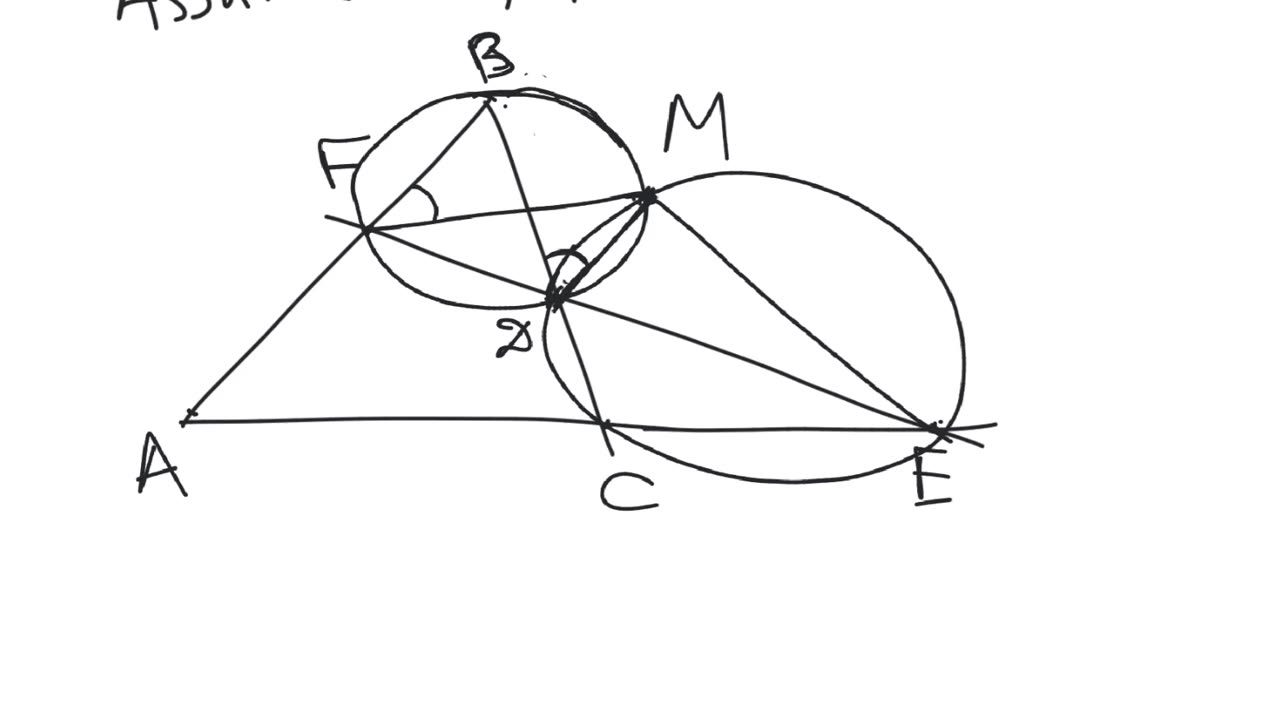
Miquel's theorem. Let $ABC$ be a triangle. Let $D$, $E$, $F$ be arbitrary points on the lines containing the sides $BC$, $CA$, $AB$ of the triangle $ABC$. Then the circumcircles of the triangles $AEF$, $BFD$, $CDE$ intersect at a single point $M$, which is called the Miquel's point.
Special case. The Miquel's point $M$ lies on the circumcircle of the triangle $ABC$ if and only if the points $D$, $E$, $F$ are collinear.
Mathematics. Geometry. Plane geometry.
#Mathematics #Geometry #PlaneGeometry
The same video on YouTube:
https://youtu.be/GOqDf2rtswQ
The same video on Telegram:
https://t.me/mathematical_bunker/146
-
 16:30
16:30
SNEAKO
16 hours agoNO FRIENDS IN THE INDUSTRY.
103K27 -
 6:19
6:19
BlackDiamondGunsandGear
1 day agoHow Fat Guys can Appendix Carry
71.3K10 -
 6:58
6:58
Gun Owners Of America
1 day ago2024 Was Huge For Gun Rights, Here's Our Top 10 Wins!
59K4 -
 15:50
15:50
Degenerate Jay
1 day ago $2.26 earnedJames Bond Is Being Ruined By Amazon? Make Him A Black Gay Woman?
44.2K11 -
 15:18
15:18
DeVory Darkins
1 day ago $18.74 earnedTrump Drops NIGHTMARE Warning on Joe Biden
59.1K102 -
 36:13
36:13
The Why Files
1 month agoAlien Implants Vol. 1: Devil’s Den UFO Encounter: What Was Found Inside Terry Lovelace?
82.9K40 -
 9:03
9:03
Alabama Arsenal
1 day ago $0.81 earnedAAC HUB 2K | Modern Features, Iconic Classic Looks
20.3K1 -
 13:49
13:49
Dermatologist Dr. Dustin Portela
2 days ago $1.57 earnedDermatologist Reveals the Worst Things To Do To Your Skin
16.5K9 -
 1:02:24
1:02:24
PMG
1 day ago $0.59 earned"Hannah Faulkner and Jamie Villamor | DEFEND, INSPIRE, INFLUENCE"
13.1K -
 44:27
44:27
BIG NEM
20 hours agoWOULD YOU RATHER? Live Stream
8.51K1