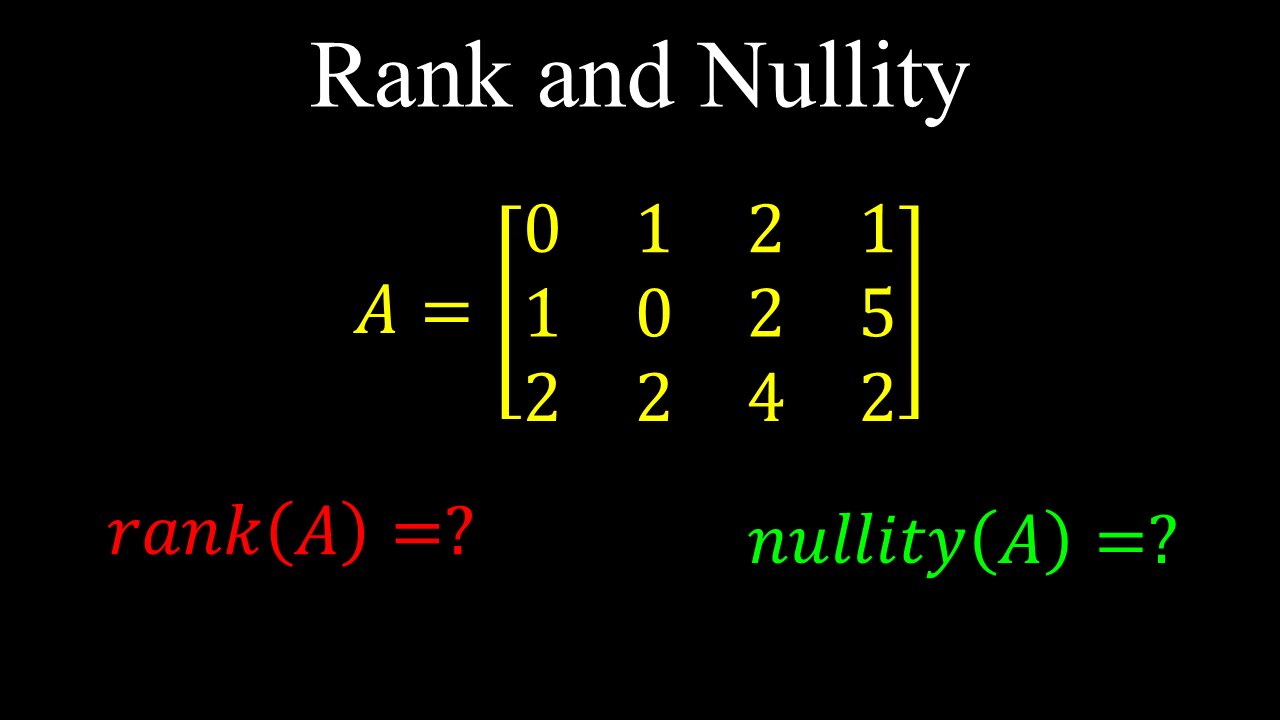
Rank and Nullity of a Matrix, Overdetermined Systems, Orthogonal Complements - Linear Algebra

This video explains the rank and nullity of a matrix (e.g. 3x3, 2x2, 4x6), including the formula, questions and examples. The nullity is the dimension of the null space of a matrix (e.g. 3x5) and can be zero. The difference between overdetermined and underdetermined systems and what it means to be inconsistent. Orthogonal complements are also covered, what is meant by them, and why the row space is the complement of the nullspace. The fundamental vector spaces of a matrix and its transpose are also explained.

0:00 Rank and nullity of a matrix
3:31 Parameters in the general solution of a non-homogeneous system
5:37 Overdetermined systems
8:33 Underdetermined systems
11:56 Fundamental matrix spaces
14:57 Orthogonal Complements