The Bevan point of a triangle | plane geometry | intermediate level

Repost
1 month ago
31
Science mathematics geometry plane geometry classical geometry Euclidean geometry triangle line triangle center Bevan Bevan point

Episode 115.

The Bevan point of a triangle | plane geometry | intermediate level.

Branch of mathematics: plane geometry.
Difficulty level: intermediate.

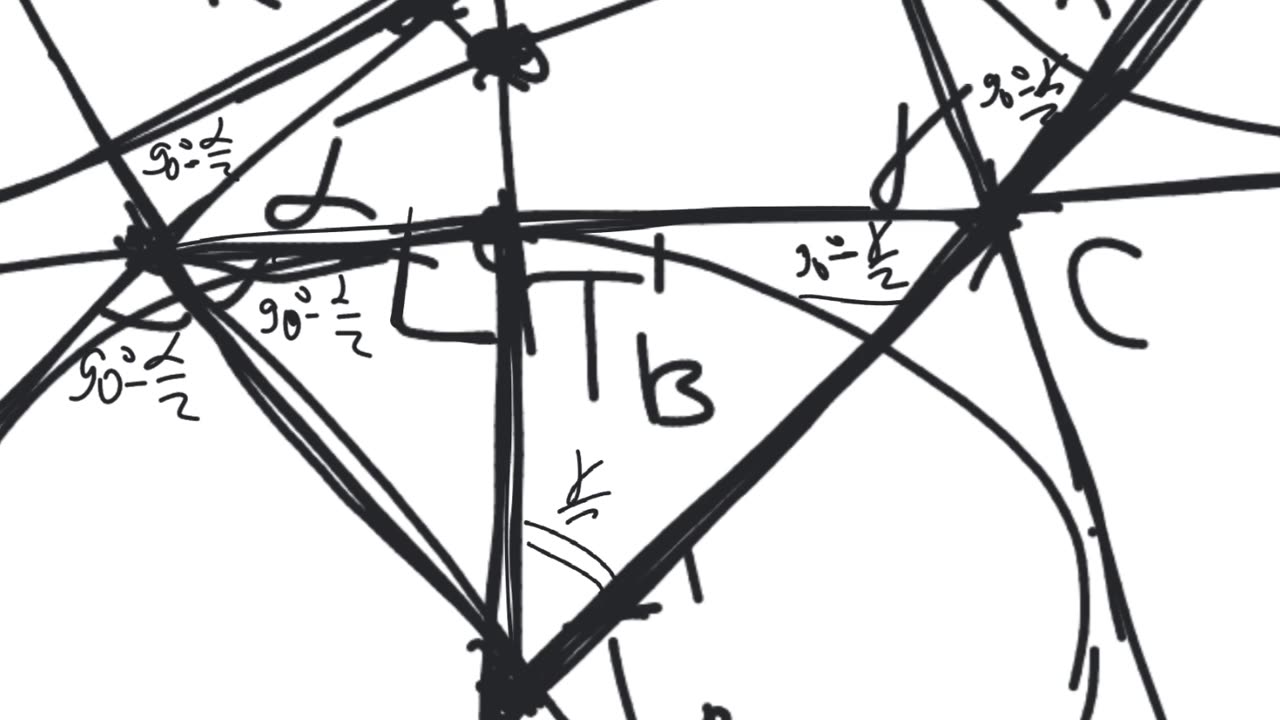
Theorem 1. Let $ABC$ be a triangle. Let $I_A$, $I_B$, $I_C$ be the centers of the excircles of the triangle $ABC$ and let $T_A'$, $T_B'$, $T_C'$ be the tangency points of those excircles with the sides. Then the lines $I_AT_A'$, $I_BT_B'$, $I_CT_B'$ intersect at a single point (which is called the Bevan point of the triangle $ABC$).

Mathematics. Geometry. Plane geometry.
#Mathematics #Geometry #PlaneGeometry

The same video on YouTube:
https://youtu.be/n9wnTmq2qdM

The same video on Telegram:
https://t.me/mathematical_bunker/140

Loading comments...