Premium Only Content
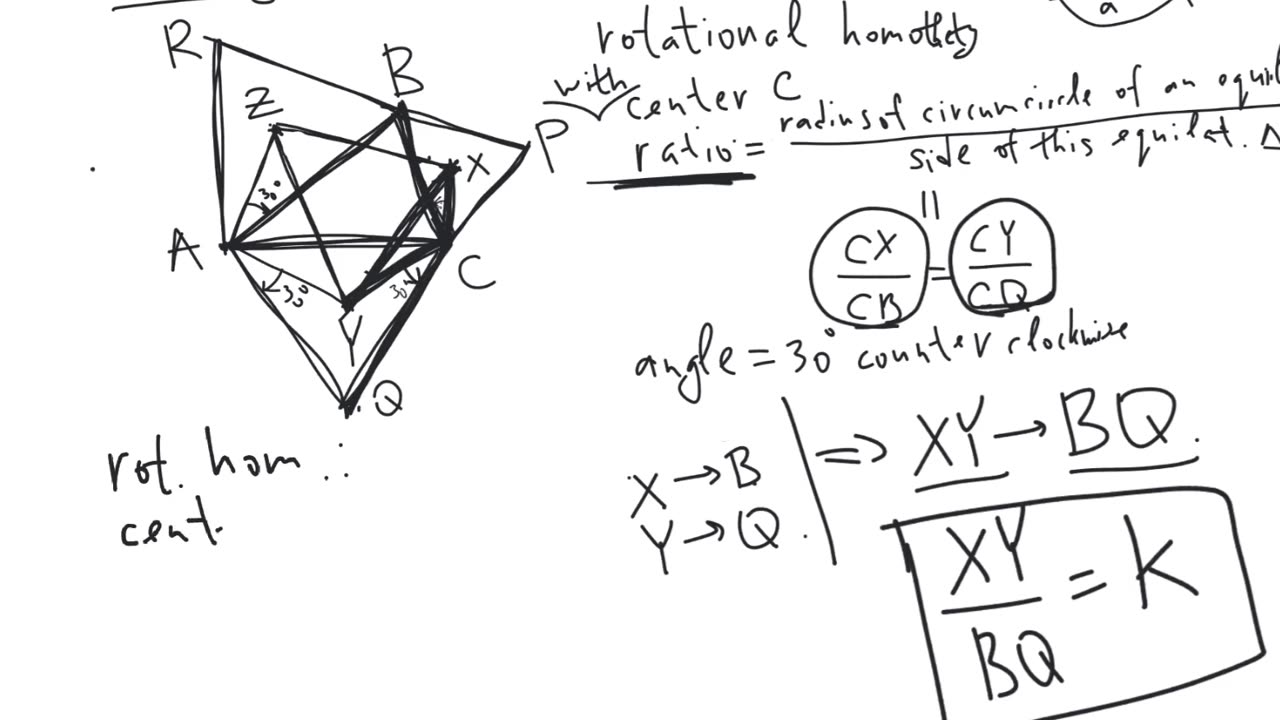
The proof of Napoleon's theorem using rotational homothety | plane geometry | advanced level
Episode 114.
The proof of Napoleon's theorem using rotational homothety | plane geometry | advanced level.
Branch of mathematics: plane geometry.
Difficulty level: advanced.
Theorem 1. Let $ABC$ be a triangle. Let $BCP$, $CAQ$, $ABR$ be equilateral triangles constructed on the sides of the triangle $ABC$ to the outside. Let $X$, $Y$, $Z$ be the centers of these equilateral triangles respectively. Then the triangle $XYZ$ is itself equilateral.
Theorem 2. Let $ABC$ be a triangle. Let $BCP'$, $CAQ'$, $ABR'$ be equilateral triangles constructed on the sides of the triangle $ABC$ to the inside. Let $X'$, $Y'$, $Z'$ be the centers of these equilateral triangles respectively. Then the triangle $X'Y'Z'$ is itself equilateral.
Mathematics. Geometry. Plane geometry.
#Mathematics #Geometry #PlaneGeometry
The same video on YouTube:
https://youtu.be/9d2G7vWw4L8
The same video on Telegram:
https://t.me/mathematical_bunker/139
-
 11:35
11:35
China Uncensored
23 hours agoChina Nuclear Fusion Breakthrough Shocks The World
2.18K14 -
 50:19
50:19
AlaskanBallistics
16 hours ago $0.12 earnedI Love This Gun Podcast Episode 6
1.86K -
 16:35
16:35
DEADBUGsays
1 day agoPolice Stories Ep4
331 -
 6:15
6:15
RTT: Guns & Gear
1 day ago $0.02 earnedSaying Goodbye To A Legend - Demolition Ranch Leaving YouTube
1934 -
 1:33:27
1:33:27
Michael Franzese
19 hours agoWhat's Elon Musk's NEXT BIG Plan?
35K30 -
 1:21:15
1:21:15
Tactical Advisor
4 hours agoThe Vault Room Podcast 008 | PSA Changing the Firearms Game and Trump Exposing Government Spending
67.7K20 -
 3:09:57
3:09:57
LittleDude games
8 hours agoSaturday Fortnite Hunters // LittleDude
54K8 -
 14:34
14:34
Misha Petrov
18 hours agoTikTok’s WOKE “Mean Girl” Is Insufferable
61.7K80 -
 10:46
10:46
Mike Rowe
1 day agoRiley Gaines Was Right All Along | The Way I Heard It with Mike Rowe
92.7K86 -
 25:19
25:19
SB Mowing
1 day agoI had to do a DOUBLE TAKE because I couldn’t see the house at first
53.6K26