Premium Only Content
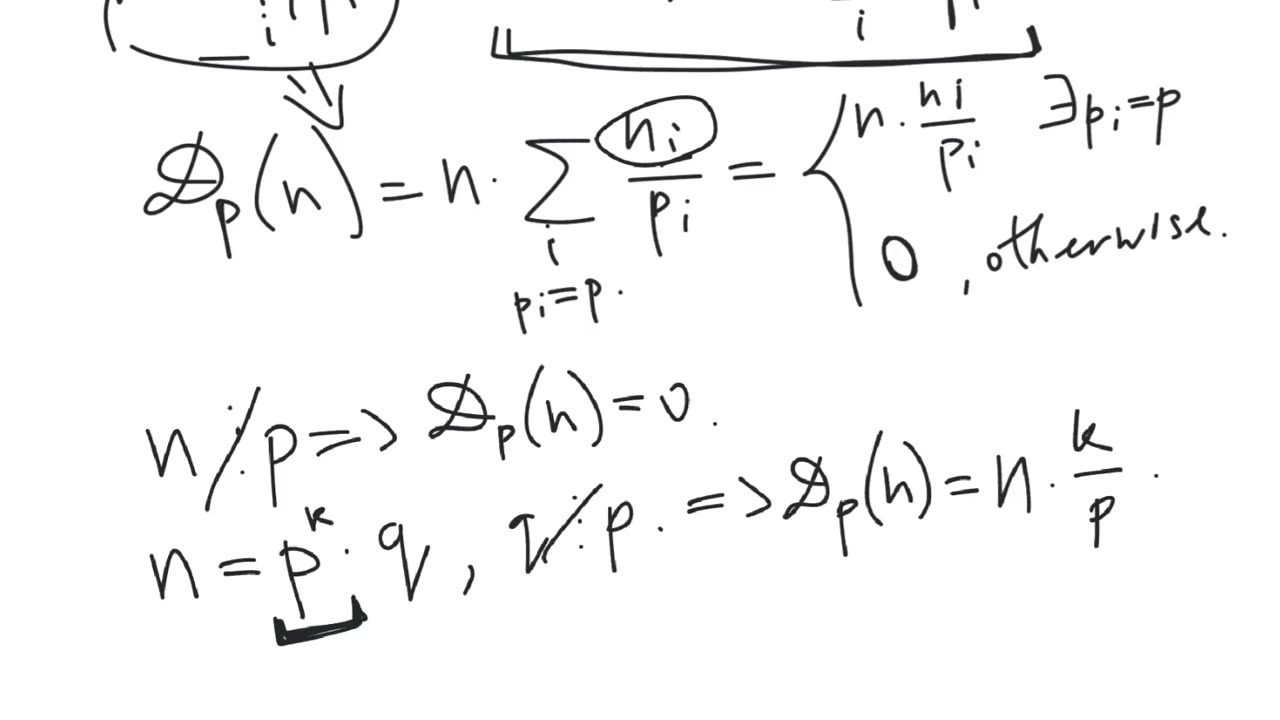
Arithmetic partial derivative | number theory | advanced level
Episode 107.
Arithmetic partial derivative | number theory | advanced level.
Branch of mathematics: number theory.
Difficulty level: advanced.
The arithmetic derivative is a function $D$ from natural numbers to natural numbers defined by the 2 properties:
1. For any prime number $p$, we have $D(p)=1$.
2. For any 2 natural numbers $m$ and $n$, we have $D(m \cdot n) = D(m) \cdot n + m \cdot D(n)$.
For a fixed prime number $p$, the arithmetic partial derivative is a function $D_p$ from natural numbers to natural numbers defined by the 2 properties:
1. We have $D_p(p) = 1$. And, for any prime number $q$, $q \neq p$, we have $D_p(q)=0$.
2. For any 2 natural numbers $m$ and $n$, we have $D(m \cdot n) = D(m) \cdot n + m \cdot D(n)$.
Theorem. If $n = p^k \cdot q$, where $q$ is not divisible by $p$, then $D_p(n)=n \cdot \frac{k}{p}$.
Theorem. For any natural number $n$, we have $D(n) = \sum_{p, \text{$p$ is prime}}{D_p(n)}$.
Mathematics. Number theory.
#Mathematics #NumberTheory
The video on YouTube:
https://youtu.be/Z_knP4RNuME
The same video on Telegram:
https://t.me/mathematical_bunker/132
-
 47:26
47:26
BonginoReport
2 hours agoEpstein Files Drop Today-But How Much Will They Reveal? (Ep.149) - 02/27/2025
25.5K69 -
 LIVE
LIVE
Wendy Bell Radio
5 hours agoThe Left Is Wrong About Everything
12,497 watching -
 29:05
29:05
CatfishedOnline
18 hours ago $0.31 earnedThe Real Jennifer Aniston or Another Romance Scam?
5.94K6 -
 34:44
34:44
LFA TV
5 days agoMIRACLES DO HAPPEN!
10.3K3 -
 16:43
16:43
T-SPLY
3 hours agoCNN Panel Member Forgets Donald Trump Runs The Military
7.34K14 -
 31:13
31:13
World Nomac
22 hours agoAMERICAN visits IRAN for 10 days (this is what I found) 🇮🇷
7.25K2 -
 1:03:55
1:03:55
The Tom Renz Show
10 hours agoBongino In At FBI & Is Factory Meat Made of Cancer?
15.1K5 -
 7:03
7:03
Dangerous Freedom
17 hours ago $0.03 earnedBest Tiny Budget Red Dot? (Honest Review - Gideon Optics Judge).
4.46K1 -
 10:32
10:32
ariellescarcella
13 hours ago"Being Trans Made Me Gay" : Hormone Science Explained
7.15K9 -
 1:02:09
1:02:09
PMG
10 hours ago $0.27 earnedTrump to BAN the COVID Vaxx?! mRNA in Your Organic Meat?! w/ Kim Bright
4.13K3