11 days ago

Science mathematics number theory prime prime number arithmetic derivative derivative differentiate differentiation product rule integer

Episode 106.

Quotient rule and extending arithmetic derivative to rational numbers | number theory | advanced.
The quotient rule for the arithmetic derivative and extending the arithmetic derivative to the rational numbers | number theory | advanced level.

Branch of mathematics: number theory.
Difficulty level: advanced.

The arithmetic derivative is a function $D$ from natural numbers to natural numbers defined by the 2 properties:
1. For any prime number $p$, we have $D(p)=1$.
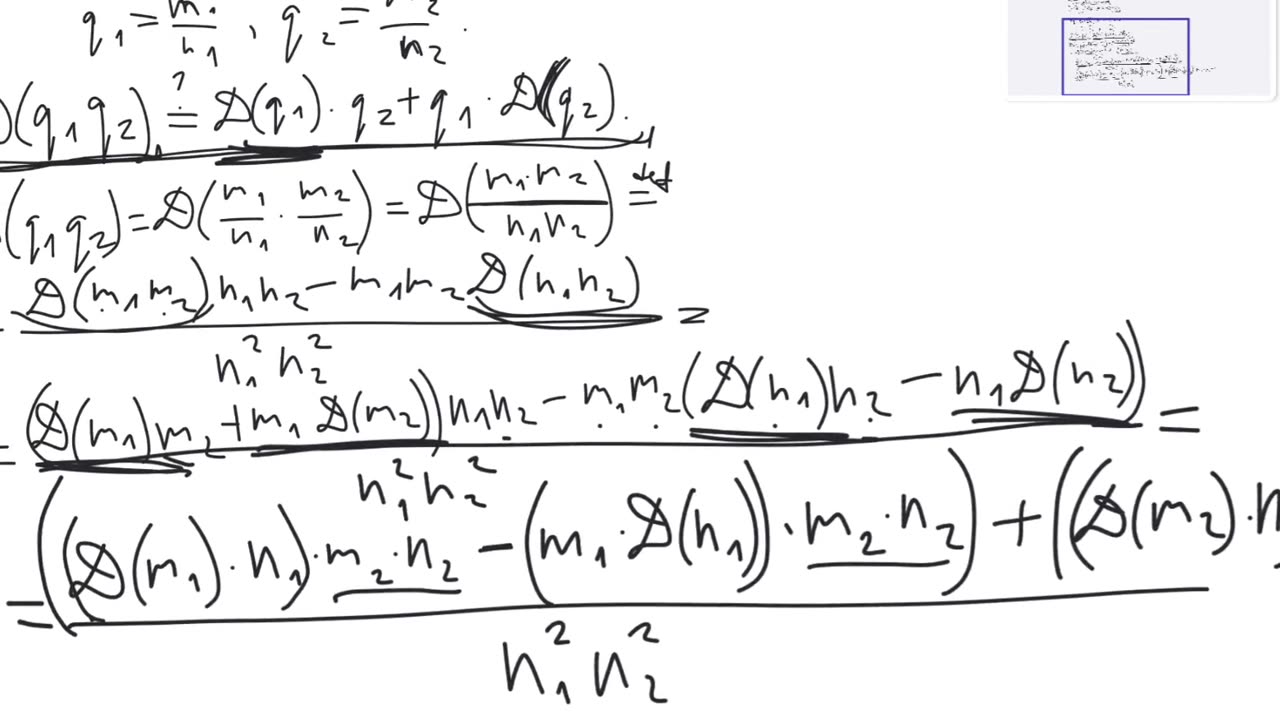
2. For any 2 natural numbers $m$ and $n$, we have $D(m \cdot n) = D(m) \cdot n + m \cdot D(n)$.

It can be proven that the quotient rule holds: for any natural numbers $m$ and $n$ such that $m$ is divisible by $n$, we have $D(\frac{m}{n})=\frac{D(m)n-mD(n)}{n^2}$.

The quotient rule also holds for integer numbers for the extension of $D$ to integer numbers.

It can be extended to all rational numbers using this quotient rule as a definition: for any rational number $q$ expressed as $q=\frac{m}{n}$ for integer numbers $m$ and $n$, we define $D(q)=\frac{D(m)n-mD(n)}{n^2}$. It can be proven that this definition is correct (that is, it does not depend on the choice of $m$ and $n$ for the same $q$), and that, with this definition, the product rule holds for all rational numbers.