Premium Only Content
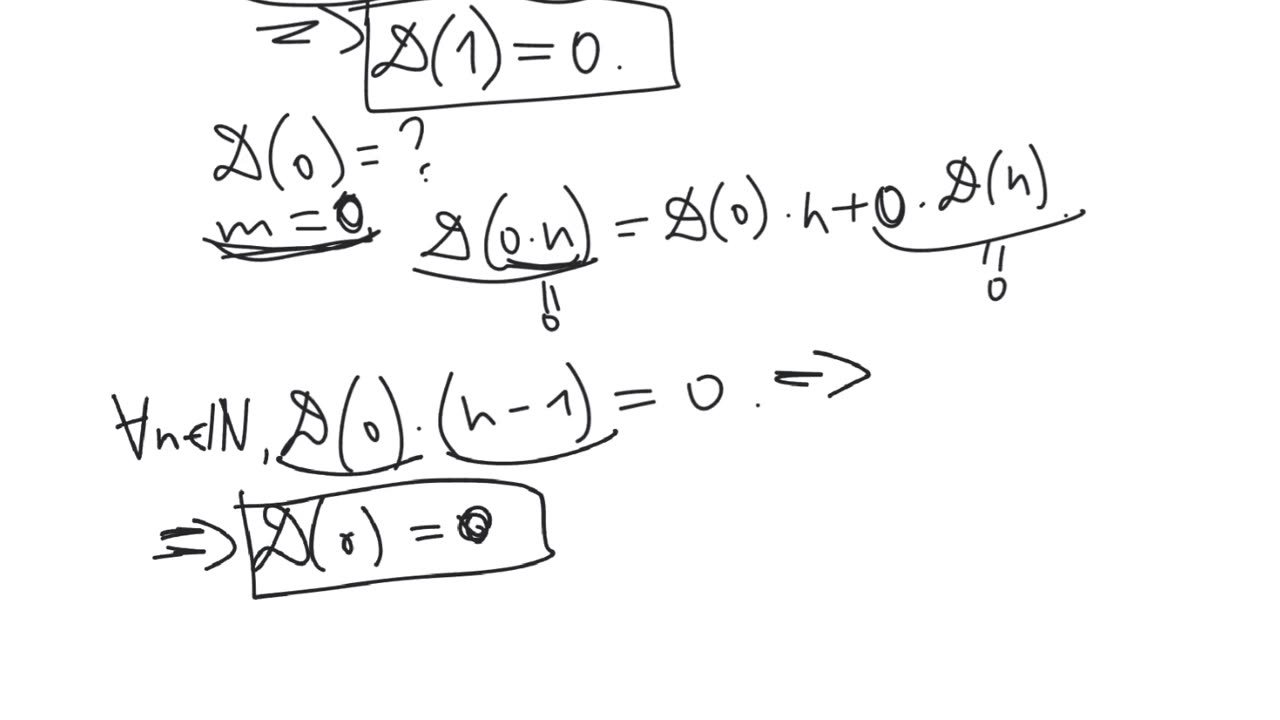
Extending the arithmetic derivative to negative numbers | number theory | advanced level
Episode 105.
Extending the arithmetic derivative to negative numbers | number theory | advanced level.
Branch of mathematics: number theory.
Difficulty level: advanced.
The arithmetic derivative is a function $D$ from natural numbers to natural numbers defined by the 2 properties:
1. For any prime number $p$, we have $D(p)=1$.
2. For any 2 natural numbers $m$ and $n$, we have $D(m \cdot n) = D(m) \cdot n + m \cdot D(n)$.
It can be proved that $D(1)=0$.
It can be extended to all integer numbers (to negative numbers and zero) like this: $D(0)=0$ and $D(-n)=-D(n)$ for any natural number $n$.
Mathematics. Number theory.
#Mathematics #NumberTheory
The same video on YouTube:
https://youtu.be/RDZzw4XnnY4
The same video on Telegram:
https://t.me/mathematical_bunker/130
-
 2:13:05
2:13:05
The Nerd Realm
15 hours ago $6.26 earnedNew Years Eve! Fortnite Hunters w/ YOU! Creator Code: NERDREALM
68.4K5 -
 11:04:44
11:04:44
FusedAegisTV
1 day agoNYE Eve! - 2025 Incoming 🎉 - 12hr Variety Stream!
133K7 -
 1:18:52
1:18:52
Awaken With JP
18 hours agoSomehow The World DIDN’T End This Year! - LIES Ep 72
167K93 -
 1:19:34
1:19:34
Michael Franzese
16 hours agoWhat 2024 Taught Us About the Future?
133K33 -
 1:48:09
1:48:09
The Quartering
16 hours agoBird Flu PANIC, Sam Hyde DESTROYS Elon Musk & Patrick Bet David & Woke Witcher?
139K80 -
 4:47
4:47
SLS - Street League Skateboarding
3 days agoLiz Akama’s 2nd Place Finish at SLS Tokyo 2024 | Best Tricks
61.7K6 -
 4:06:54
4:06:54
LumpyPotatoX2
15 hours agoHappy New Year Rumble ! - #RumbleGaming
44.9K1 -
 10:37
10:37
One Bite Pizza Reviews
1 day agoBest of Barstool Pizza Reviews 2024
69.8K32 -
 2:37
2:37
Tate Speech by Andrew Tate
17 hours ago2025 WILL BE YOUR YEAR
119K44 -
 3:51:31
3:51:31
Sgtfinesse
18 hours agoRumble New Years Eve with Sarge
69.5K