Premium Only Content
Van Aubel's theorem about cevians | plane geometry | intermediate level
Episode 89.
Van Aubel's theorem about cevians | plane geometry | intermediate level.
Branch of mathematics: plane geometry.
Difficulty level: intermediate.
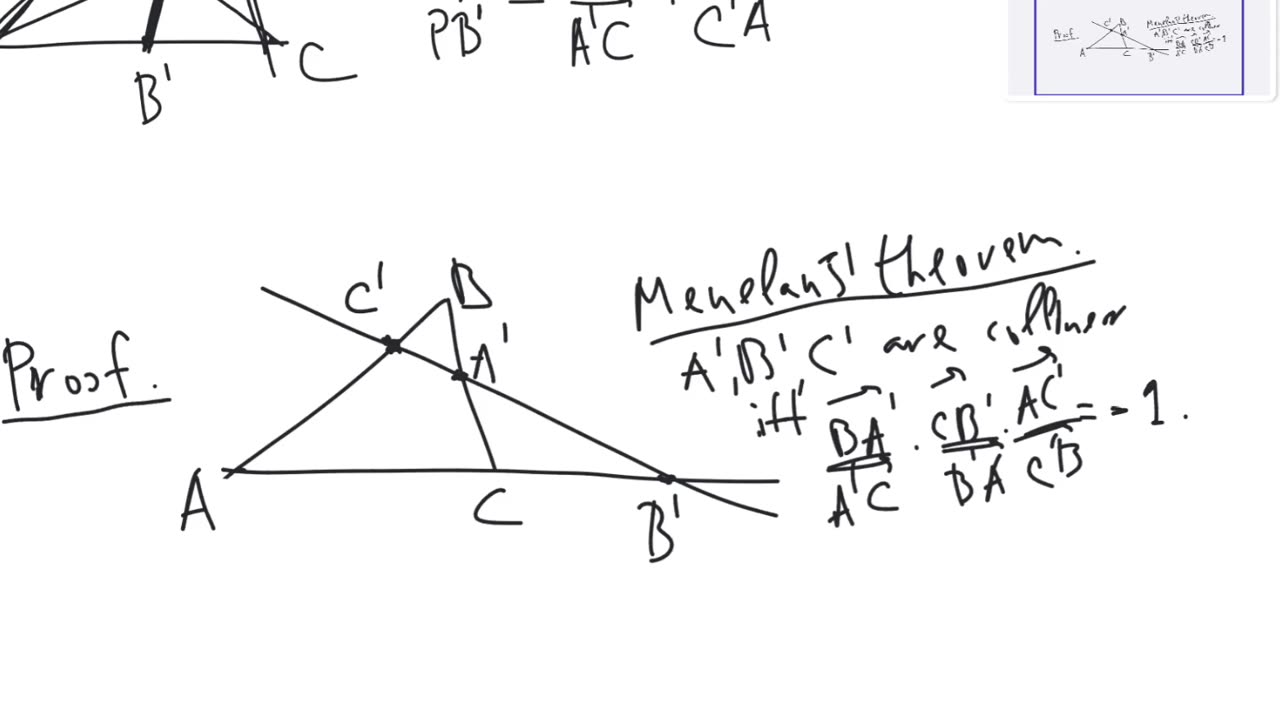
Van Aubel's theorem about cevians. Let $ABC$ be a triangle. Let $AA'$, $BB'$, $CC'$ be cevians for point $P$ (that is, let $A'$, $B'$, $C'$ be points on the lines $BC$, $CA$, $AB$ respectively such that the lines $AA'$, $BB'$, $CC'$ intersect at a single point $P$). Then $\frac{\overrightarrow{BP}}{\overrightarrow{PB'}} = \frac{\overrightarrow{BA'}}{\overrightarrow{A'C}} + \frac{\overrightarrow{BC'}}{\overrightarrow{C'A}}$.
Mathematics. Geometry. Plane geometry.
#Mathematics #Geometry #PlaneGeometry
The same video on YouTube:
https://youtu.be/pG18wIqS5Rg
The same video on Telegram:
https://t.me/mathematical_bunker/112
-
 10:31:05
10:31:05
Dr Disrespect
15 hours ago🔴LIVE - DR DISRESPECT - PGA TOUR 2K25 LAUNCH DAY
184K27 -
 2:30:04
2:30:04
Laura Loomer
6 hours agoEP105: MISSING: The Epstein Files
56.9K20 -
 1:46:14
1:46:14
Kim Iversen
7 hours agoTrump to Zelenskyy: 'You're Gambling with World War III'
67.8K107 -
 55:28
55:28
Glenn Greenwald
8 hours agoGlenn Reacts to Trump-Zelensky Exchange and Takes Q&A from our Members | SYSTEM UPDATE #415
111K197 -
 4:26:54
4:26:54
Nerdrotic
11 hours ago $34.34 earnedMarvel PANIC MODE! Kathleen Kennedy GONE?! Hollywood DEI Dead | Friday Night Tights 342 Nick Freitas
127K36 -
 1:30:03
1:30:03
Flyover Conservatives
1 day agoZelensky Fail... God Called IT!; From Prison to the White House: Angela Stanton King’s Unbelievable Redemption Story | FOC Show
45.9K6 -
 1:06:14
1:06:14
IsaacButterfield
10 hours ago $2.00 earnedFree Speech Is Dead | Did Trump Go Too Far? | Sexist Job
41.4K18 -
 1:02:59
1:02:59
Sarah Westall
13 hours agoEpstein Files, Dueling Cabal Factions and Gold from Ancient Civilizations w/ Dave Hodges
71K19 -
 3:15:08
3:15:08
I_Came_With_Fire_Podcast
11 hours ago“Trump-Zelensky BEATDOWN | Europe BUILDS MUSCLE | NEWSCUM Podcast”
17.4K1 -
 41:25
41:25
CatfishedOnline
11 hours ago $1.84 earned23-Yr-Old Drove 2,650 Miles to Meet Online Girlfriend in Romance Scam
40.1K4