Premium Only Content
Desargues' theorem | plane geometry | intermediate level
Episode 88.
Desargues' theorem | plane geometry | intermediate level.
Branch of mathematics: plane geometry.
Difficulty level: intermediate.
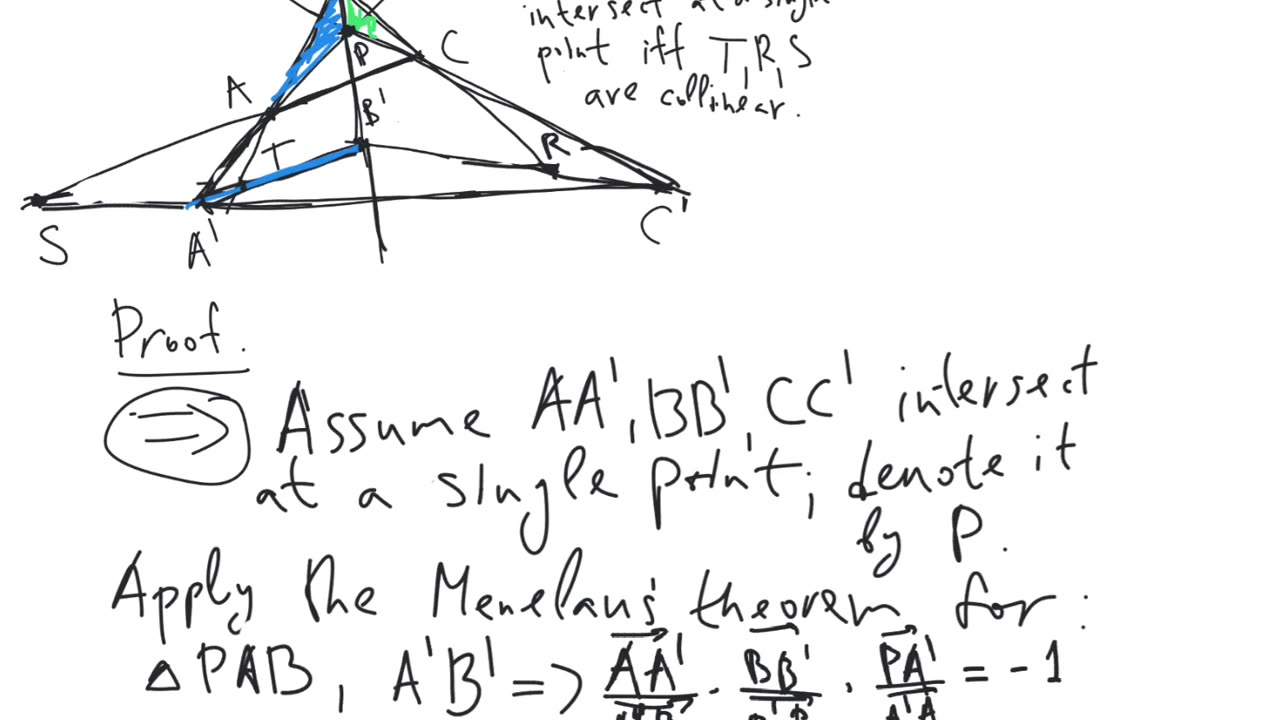
Desargues' theorem. Let $ABC$ and $A'B'C'$ be triangles. Then the intersection points of the lines containing the corresponding sides of the triangles (the intersection points of the lines $AB$ and $A'B'$, of the lines $BC$ and $B'C'$, of the lines $CA$ and $C'A'$) are collinear or these 3 pairs of lines are all parallel (inside the pairs, but not necessarily between the pairs; so, $AB \parallel A'B'$, $BC \parallel B'C'$, $CA \parallel C'A'$) if and only if the lines connecting the corresponding vertices of the triangles (the lines $AA'$, $BB'$, $CC'$) intersect at a single point or all 3 are parallel to each other.
Notice that, in the video, I forgot the special cases of parallel lines.
Mathematics. Geometry. Plane geometry.
#Mathematics #Geometry #PlaneGeometry
The same video on YouTube:
https://youtu.be/GPNQzkEzd6A
The same video on Telegram:
https://t.me/mathematical_bunker/111
-
 23:38
23:38
RealitySurvival
1 day agoBest Anti-Drone Rounds For Self Defense
19K3 -
 57:43
57:43
barstoolsports
17 hours agoBest Shot Wins The Game | Surviving Barstool S4 Ep. 7
209K9 -
 1:52:24
1:52:24
Kim Iversen
13 hours agoLuigi Mangione Charged With TERRORISM | Liz Cheney Accused Of WITNESS TAMPERING, Faces 20 YEARS IN JAIL
114K157 -
 6:50:10
6:50:10
Akademiks
14 hours agoJay Z says he aint NEVER been friends w/ DIDDY! Bhad Bhabie lost her man? Travis Hunter Down Bad?
117K14 -
 2:27:04
2:27:04
AirCondaTv Gaming
12 hours ago $24.12 earnedWar Thunder - Tankering Around for That 10 Bomb
60.6K5 -
 4:19:05
4:19:05
SpartakusLIVE
15 hours agoThe MACHINE locks in for 12-hour POWER stream
43K1 -
 1:58:40
1:58:40
Robert Gouveia
14 hours agoJ6 Coverup: Prosecute LIZ CHENEY; NY Judge REJECTS Immunity; Trump Breaks Gag?
177K93 -
 2:22:06
2:22:06
WeAreChange
13 hours agoPSYOP Spreads: Drones Shut Down Airport In New York!
113K52 -
 1:31:18
1:31:18
Redacted News
15 hours agoEMERGENCY! NATO AND CIA ASSASSINATE TOP RUSSIAN GENERAL, PUTIN VOWS IMMEDIATE RETALIATION | Redacted
252K595 -
 56:45
56:45
VSiNLive
14 hours ago $7.26 earnedFollow the Money with Mitch Moss & Pauly Howard | Hour 1
90.5K2