Premium Only Content
Desargues' theorem | plane geometry | intermediate level
Episode 88.
Desargues' theorem | plane geometry | intermediate level.
Branch of mathematics: plane geometry.
Difficulty level: intermediate.
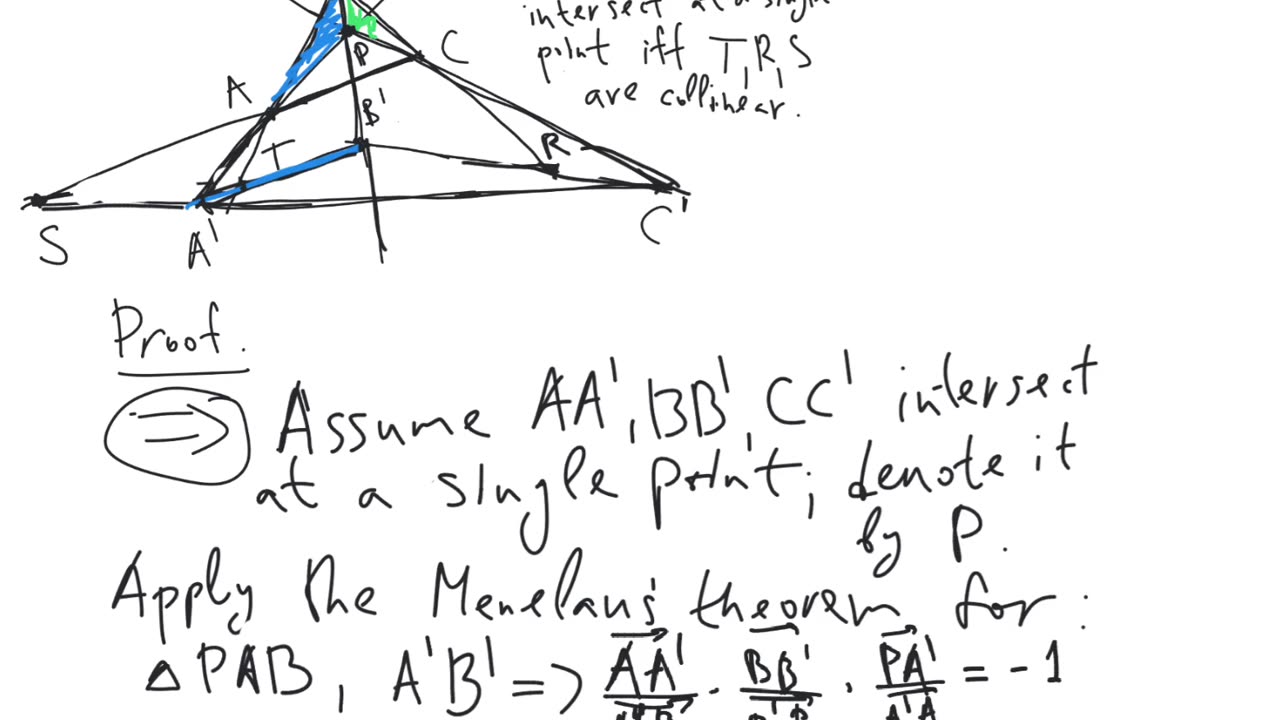
Desargues' theorem. Let $ABC$ and $A'B'C'$ be triangles. Then the intersection points of the lines containing the corresponding sides of the triangles (the intersection points of the lines $AB$ and $A'B'$, of the lines $BC$ and $B'C'$, of the lines $CA$ and $C'A'$) are collinear or these 3 pairs of lines are all parallel (inside the pairs, but not necessarily between the pairs; so, $AB \parallel A'B'$, $BC \parallel B'C'$, $CA \parallel C'A'$) if and only if the lines connecting the corresponding vertices of the triangles (the lines $AA'$, $BB'$, $CC'$) intersect at a single point or all 3 are parallel to each other.
Notice that, in the video, I forgot the special cases of parallel lines.
Mathematics. Geometry. Plane geometry.
#Mathematics #Geometry #PlaneGeometry
The same video on YouTube:
https://youtu.be/GPNQzkEzd6A
The same video on Telegram:
https://t.me/mathematical_bunker/111
-
 51:57
51:57
Professor Nez
3 hours ago🚨LAWFARE COLLAPSES? What NOBODY is Saying About Jack Smith Dismissing Trump Case
21.7K29 -
 LIVE
LIVE
GussyWussie
6 hours agoReturning to one of the Best Zelda Games - Breath of the Wild
545 watching -
 2:33:50
2:33:50
Wahzdee
3 hours agoMorning Grind: Arena Breakout vs Tarkov Showdown 🎮 - Wahzvember Day 25
34.4K2 -
 0:41
0:41
World Nomac
18 hours agoThe side of Las Vegas they don't want you to know about
23.9K1 -
 LIVE
LIVE
Film Threat
7 hours agoVERSUS: WICKED VS GLADIATOR II | Film Threat Versus
298 watching -
 2:06:30
2:06:30
Barstool Yak
8 hours agoThe Yak with Big Cat & Co. Presented by Rhoback | The Yak 11-25-24
24.6K3 -
 1:43:44
1:43:44
The Quartering
6 hours agoDr Disrespect Leaves Youtube For Rumble! With Rumble CEO Chris Pavlovski
112K61 -
 50:55
50:55
Grant Stinchfield
3 hours ago $1.97 earnedMy Trip To The Emergency Room Exposed the Our Joke of a Health Care System
16.4K3 -
 2:50:00
2:50:00
RyanMatta
1 day ago $3.00 earnedOPERATION AMBER ALERT | CHILD TRAFFICKING DOCUMENTARY | EXECUTIVE PRODUCER RYAN MATTA
14.3K16 -
 14:14
14:14
TimcastIRL
1 day agoJoe Rogan ROASTS The View For Saying He BELIEVES IN DRAGONS In HILARIOUS MOCKERY
53.2K82