Premium Only Content
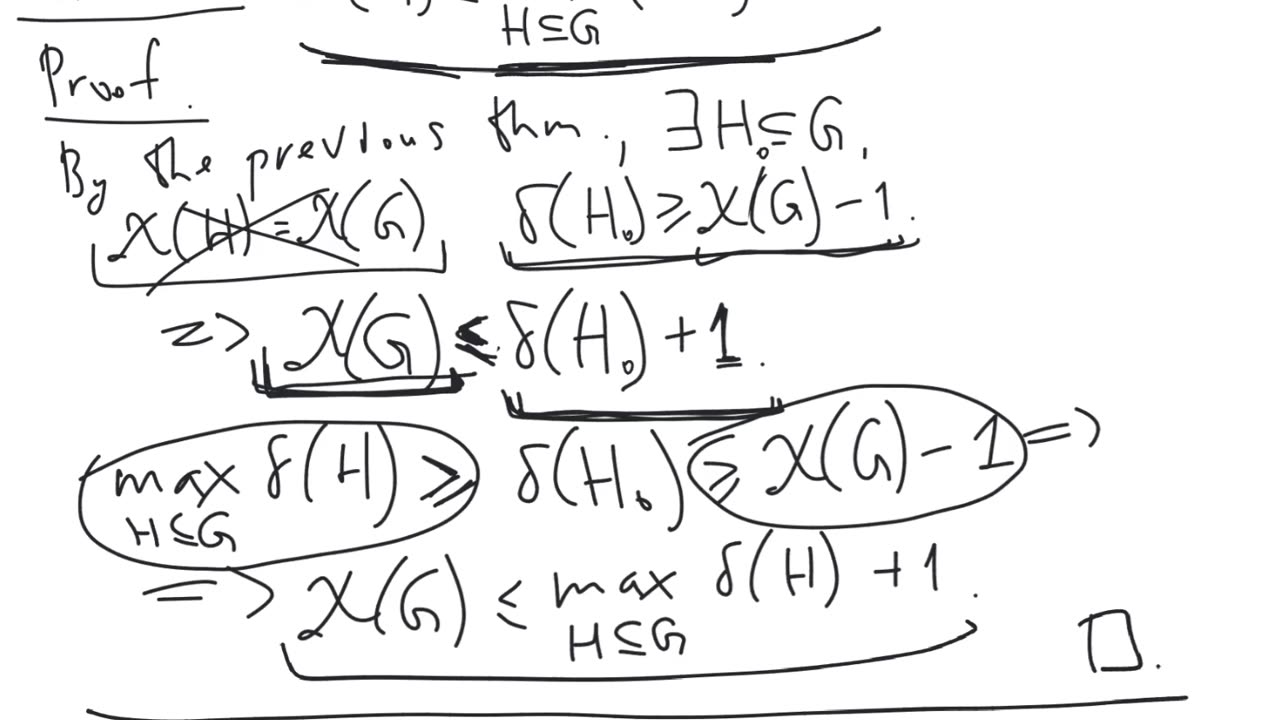
The chromatic number of a graph and min degrees of its subgraphs | graph theory | intermediate level
Episode 86.
The chromatic number of a graph and min degrees of its subgraphs | graph theory | intermediate level.
The connection between the chromatic number of a graph and the minimum degrees of its subgraphs | graph theory | intermediate level.
Branch of mathematics: graph theory.
Difficulty level: intermediate.
Theorem. Any graph $G$ contains a subgraph $H$ with $\Chi(H)=\Chi(G)$ and $\delta(H) \geq \Chi(G) - 1$.
Theorem. For any graph $G$, there is an upper bound on the chromatic number of $G$ in terms of the minimum degrees of its subgraphs: $\Chi(G) \leq \max_{H \subseteq G}{(\delta(H))} + 1$.
Mathematics. Discrete Mathematics. Combinatorics. Graph theory.
#Mathematics #DiscreteMathematics #Combinatorics #GraphTheory
The same video on YouTube:
https://youtu.be/e6k6UTaYm48
The same video on Telegram:
https://t.me/mathematical_bunker/110
-
 LIVE
LIVE
megimu32
3 hours agoON THE SUBJECT: IRL Streamers Attacked & Nostalgic Animal Movies That Made Us Cry
601 watching -
 1:00:54
1:00:54
The Tom Renz Show
7 hours agoMore Epstein/FBI, a Scary Trade War, & the Dem Echo Chamber
7.49K1 -
 40:43
40:43
Kimberly Guilfoyle
8 hours agoDems Double Down on Delusion-Why? Live with Tony Kinnett & Bo French | Ep.202
77.8K35 -
 1:28:42
1:28:42
Redacted News
6 hours agoBREAKING! SOMETHING BIG IS HAPPENING IN EUROPE ALL OUT WAR IS COMING AGAINST RUSSIA, TRUMP FURIOUS
121K282 -
 47:50
47:50
Candace Show Podcast
6 hours agoBREAKING: Judge Makes Statement Regarding Taylor Swift's Text Messages. | Candace Ep 155
113K112 -
 1:14:23
1:14:23
Josh Pate's College Football Show
3 hours ago $0.29 earnedCFB’s Most Hated Teams | FSU & Clemson Future | Big Ten Win Totals | Star Rankings Overrated?
14.5K -
 1:33:47
1:33:47
CatfishedOnline
5 hours agoGoing Live With Robert - Weekly Recap
27.8K -
 55:18
55:18
LFA TV
1 day agoEurope’s Sudden Turn Against America | TRUMPET DAILY 3.6.25 7PM
32.2K3 -
 4:21
4:21
Tundra Tactical
4 hours ago $2.12 earnedPam Bondi MUST Enforce Due Process NOW!
23.7K1 -
 56:42
56:42
VSiNLive
5 hours agoFollow the Money with Mitch Moss & Pauly Howard | Hour 1
48K1