Premium Only Content
This video is only available to Rumble Premium subscribers. Subscribe to
enjoy exclusive content and ad-free viewing.
Ceva's theorem | plane geometry | intermediate level
3 months ago
9
Science
mathematics
geometry
plane geometry
classical geometry
Euclidean geometry
triangle
Ceva
theorem
Ceva's theorem
line
Episode 82.
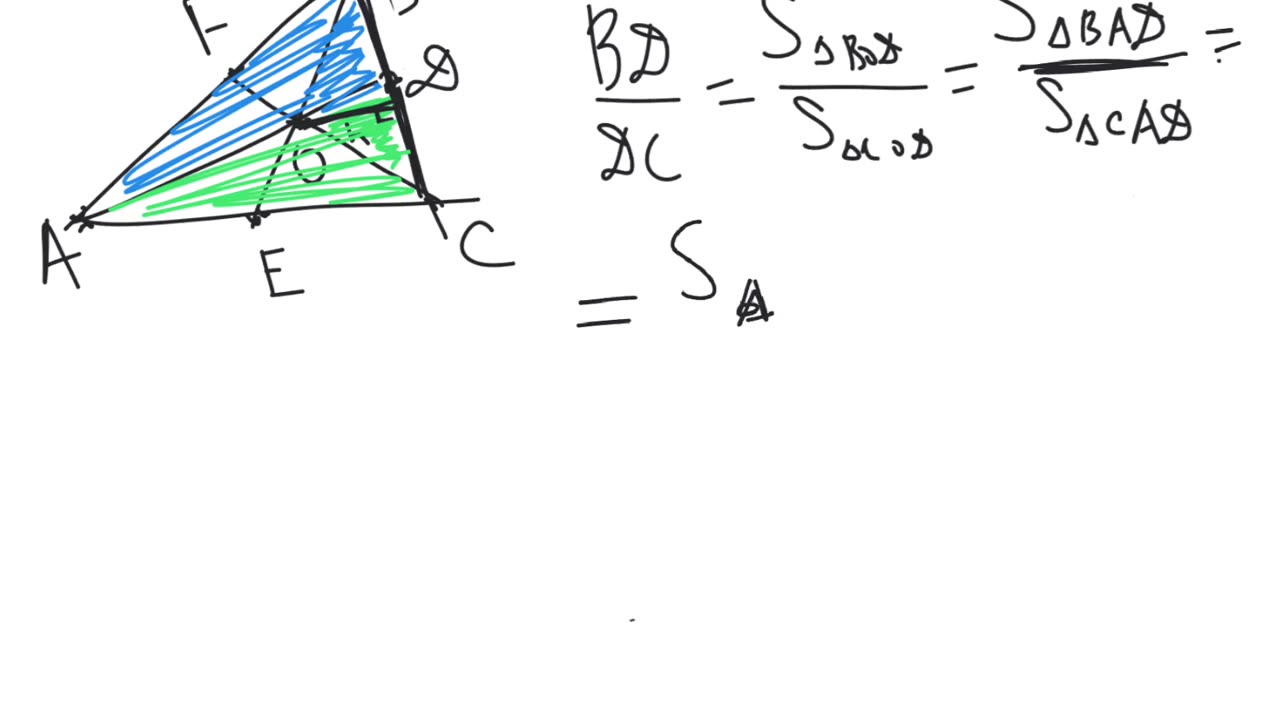
Ceva's theorem | plane geometry | intermediate level.
Branch of mathematics: plane geometry.
Difficulty level: intermediate.
Theorem. Let $ABC$ be a triangle. Let $D$, $E$, $F$ be points on the lines $BC$, $CA$, $AB$ respectively. Then the lines $AD$, $BE$, $CF$ intersect at a single point or all 3 are parallel to each other if and only if $\frac{\overrightarrow{BD}}{\overrightarrow{DC}} \cdot \frac{\overrightarrow{CE}}{\overrightarrow{EA}} \cdot \frac{\overrightarrow{AF}}{\overrightarrow{FB}} = 1$.
Mathematics. Geometry. Plane geometry.
#Mathematics #Geometry #PlaneGeometry
The same video on YouTube:
https://youtu.be/ooUZNVOJAtw
The same video on Telegram:
https://t.me/mathematical_bunker/106
Loading comments...
-
 1:52:24
1:52:24
Kim Iversen
13 hours agoLuigi Mangione Charged With TERRORISM | Liz Cheney Accused Of WITNESS TAMPERING, Faces 20 YEARS IN JAIL
114K157 -
 6:50:10
6:50:10
Akademiks
14 hours agoJay Z says he aint NEVER been friends w/ DIDDY! Bhad Bhabie lost her man? Travis Hunter Down Bad?
117K14 -
 2:27:04
2:27:04
AirCondaTv Gaming
12 hours ago $24.12 earnedWar Thunder - Tankering Around for That 10 Bomb
60.6K5 -
 4:19:05
4:19:05
SpartakusLIVE
15 hours agoThe MACHINE locks in for 12-hour POWER stream
43K1 -
 1:58:40
1:58:40
Robert Gouveia
14 hours agoJ6 Coverup: Prosecute LIZ CHENEY; NY Judge REJECTS Immunity; Trump Breaks Gag?
177K93 -
 2:22:06
2:22:06
WeAreChange
13 hours agoPSYOP Spreads: Drones Shut Down Airport In New York!
113K52 -
 1:31:18
1:31:18
Redacted News
15 hours agoEMERGENCY! NATO AND CIA ASSASSINATE TOP RUSSIAN GENERAL, PUTIN VOWS IMMEDIATE RETALIATION | Redacted
252K598 -
 56:45
56:45
VSiNLive
14 hours ago $7.26 earnedFollow the Money with Mitch Moss & Pauly Howard | Hour 1
90.5K2 -
 52:44
52:44
Candace Show Podcast
14 hours agoMy Conversation with Only Fans Model Lilly Phillips | Candace Ep 122
118K381 -
 5:47:55
5:47:55
tacetmort3m
15 hours ago🔴 LIVE - RELIC HUNTING CONTINUES - INDIANA JONES AND THE GREAT CIRCLE - PART 5
57.2K