Premium Only Content
This video is only available to Rumble Premium subscribers. Subscribe to
enjoy exclusive content and ad-free viewing.
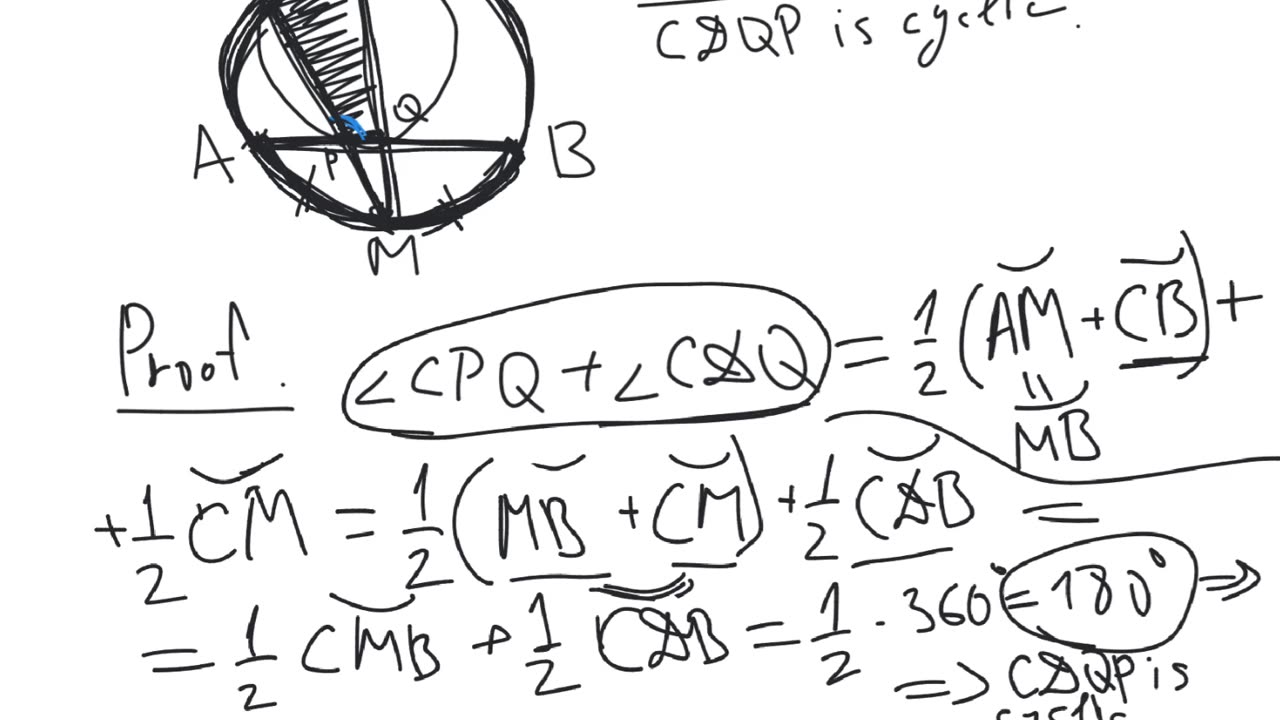
Cyclic quadrilateral formed by inscribed angle from the midpoint of an arc | geometry | intermediate
5 months ago
35
Science
mathematics
geometry
plane geometry
classical geometry
chord
circle
quadrilateral
cyclic
cyclic quadrilateral
angle
Episode 63.
Cyclic quadrilateral formed by inscribed angle from the midpoint of an arc | geometry | intermediate.
The cyclic quadrilateral formed by an inscribed angle from the midpoint of an arc intersecting the circle and the chord | plane geometry | intermediate level.
Branch of mathematics: plane geometry.
Difficulty level: intermediate.
Theorem. Let $M$ be the midpoint of an arc $AB$ of a circle. Let $CMD$ be an inscribed angle intersecting the chord $AB$ at $P$ and $Q$. Then the quadrilateral $CDQP$ is cyclic.
Mathematics. Geometry. Plane geometry.
#Mathematics #Geometry #PlaneGeometry
The same video on YouTube:
https://youtu.be/PoKvmIcubes
The same video on Telegram:
https://t.me/mathematical_bunker/87
Loading comments...
-
 47:26
47:26
The Rubin Report
2 hours agoBill Gates Makes ‘The View’ Crowd Go Quiet with This Chilling Warning
42K99 -
 2:02:40
2:02:40
Steven Crowder
4 hours agoHow USAID Spread Fake News with Your Tax Dollars & Trump Took Down Title IX
314K190 -
 LIVE
LIVE
TheAlecLaceShow
1 hour agoGuests: Alex Marlow, Rep. Cloud & Rep. Gill | No Men In Women’s Sports | The Alec Lace Show
111 watching -
 52:02
52:02
PMG
16 hours agoHannah Faulkner and Pastor Mark Driscoll | WAKE UP CHURCH
389 -
 2:07:17
2:07:17
Matt Kohrs
12 hours agoMAX DEGEN TILT!!! (New Highs Incoming!) || The MK Show
45.9K2 -
 55:35
55:35
Grant Stinchfield
1 hour agoDemocrats Fight Against Trump is a Losing Battle as the Swamp Drains Itself
9.99K5 -
 LIVE
LIVE
The Shannon Joy Show
2 hours ago🔥HUGE Victory for Sanity - Trump Signs Executive Order Banning Trans Males From Women’s Sports! With Special Guest Alex Newman!🔥
631 watching -
 53:17
53:17
The Criminal Connection Podcast
9 hours agoKING OF CLUBS: Terry Turbo Story (PART 2) One Nation: The Early Days (90'S RAVE SCENE DOCUMENTARY)
6.88K1 -
 42:40
42:40
Rethinking the Dollar
2 hours agoTrump Ignores Cali Insurance Crisis Yet Has Big Plans For Gaza
20.5K20 -
 2:58:53
2:58:53
Wendy Bell Radio
8 hours agoDOGE Just Ended The Deep State
125K71