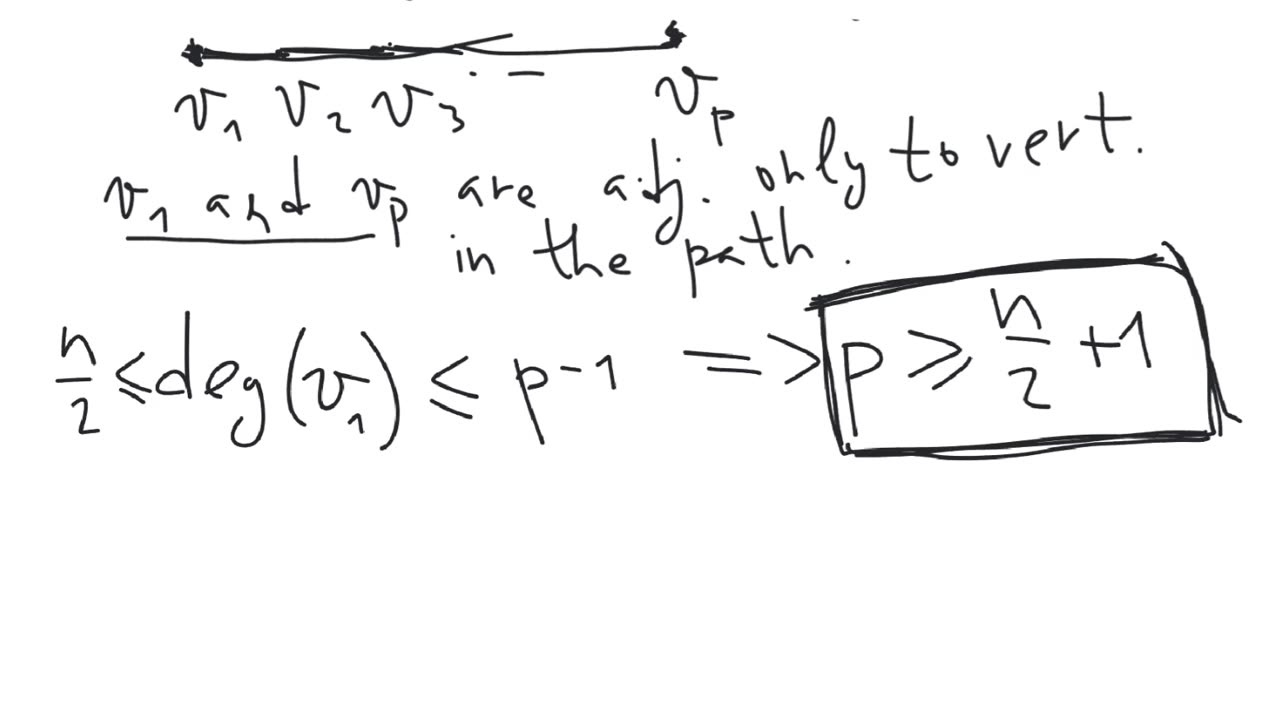
Dirac's theorem about Hamiltonian graphs | graph theory

2 months ago
37
Science mathematics graph graph theory combinatorics discrete mathematics Hamiltonian Hamiltonian graph Hamiltonian cycle cycle path

Episode 44.

Dirac's theorem about Hamiltonian graphs | graph theory.

Definition. A Hamiltonian cycle in a graph is a cycle that passes through all vertices of the graph.
Definition. A graph is said to be Hamiltonian if it has a Hamiltonian cycle.
Dirac's theorem. For any graph $G$ on $n$ vertices, where $n \geq 3$, if the degree of any vertex is greater or equal than $n/2$, then the graph $G$ is Hamiltonian.

Mathematics. Discrete Mathematics. Combinatorics. Graph theory.
#Mathematics #DiscreteMathematics #Combinatorics #GraphTheory

The same video on YouTube:
https://youtu.be/7sNdIM4F5SI

The same video on Telegram:
https://t.me/mathematical_bunker/68

Loading comments...