Startrails on a flat plane

Startrails on a flat plane
[by Shane] https://adl.place

In summary:
Imagine viewing the sky in a hemispherical manner, similar to how we perceive the globe. This sphere has a radius of 3,959 miles, and the circumference of your visible horizon would be approximately 24,901 miles.

When applying this concept to the celestial heavens, we observe a latitude-dependent pole around which stars appear to rotate. In the Northern Hemisphere, Polaris is visible, but not directly overhead unless you're at the North Pole. As you move towards the equator, both celestial poles become visible due to an optical phenomenon known as convergence.

This convergence is created by the bending of light, which makes parallel light rays appear to form a dome over the observer. During the day, the sun's rays appear to converge, and a similar effect occurs at night with star trails. These trails emanate from a singular source and warp into a concentric pattern due to perspective.

At the equator, the optical convergence point known as the South Pole becomes visible. This point is latitude-dependent and marks the area around which stars appear to rotate. As you move further south, the South Pole becomes more prominent, while the North Pole dips below the horizon.

The model used to describe this phenomenon is not to scale, but it represents a dome with a radius of 3,959 miles. When standing directly beneath the North Pole, stars appear to rotate around you in a hemispherical pattern. Moving between the North Pole and the equator, the apparent rotation point shifts.

Stellarium software uses a similar model to represent the stars, employing a coordinate system that transforms local observations into a celestial sphere. This transformation involves mapping geographic coordinates to celestial coordinates, creating a one-to-one correlation between the Earth's surface and the sky.

The explanation of star trails on a flat Earth involves understanding optical convergence, perspective, and the transformation of coordinate systems. This model attempts to reconcile observations of the sky with a flat Earth perspective, highlighting the role of latitude and optical effects in celestial phenomena.

Descript Transcript
https://share.descript.com/view/sEvgqX0bmUx

  📍 All , let's just do a quick walkthrough about how the stars and the celestial poles work on flat earth. So to start, , let's just assume that you see in globular dimensions, meaning you see in a hemisphere around you on a flat plane up to the dimensions prescribed by the globe. So in a sphere or half sphere of radius 3959.

If you were to take a circumference of the circle of the limit of your view would be about 24, 901 statute miles in a circle. Apply this to the celestial heavens and we get a latitude dependent pole around things around which things appear to rotate in the north, ? Polar stars in the north, ?

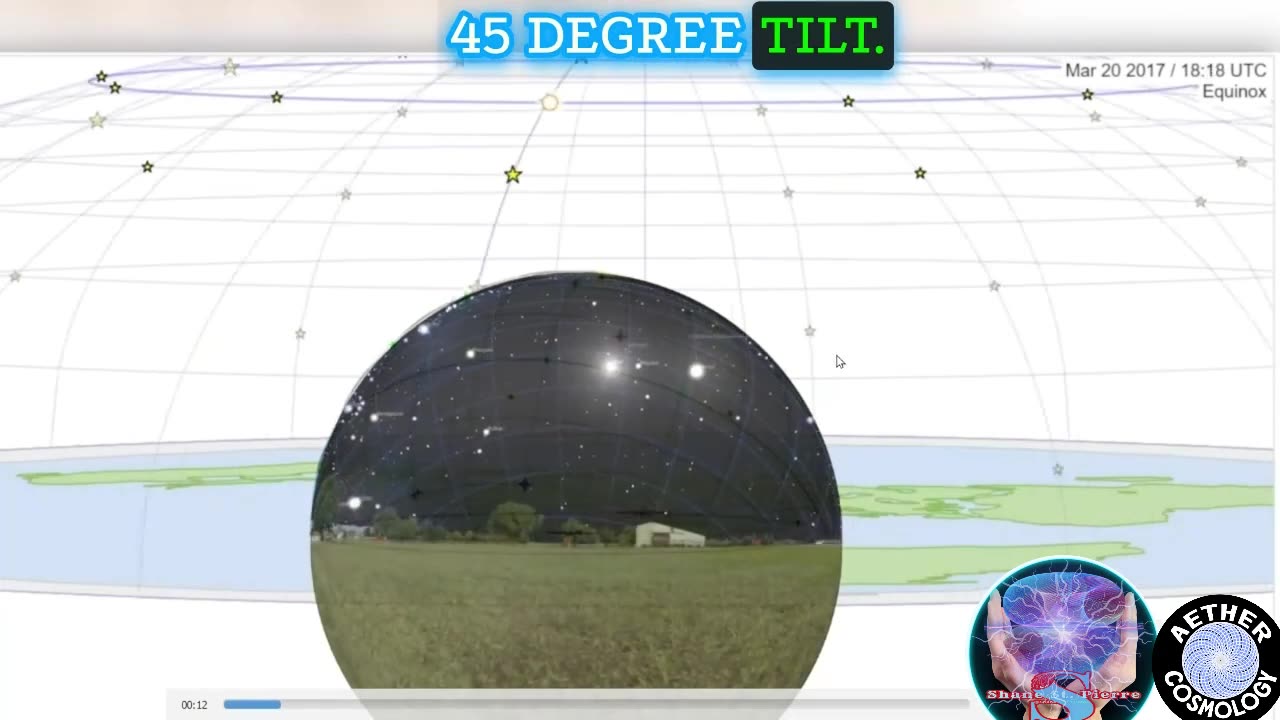
Here we have a 45 degree tilt. Someone is in northern latitude looking at the stars. This is what they