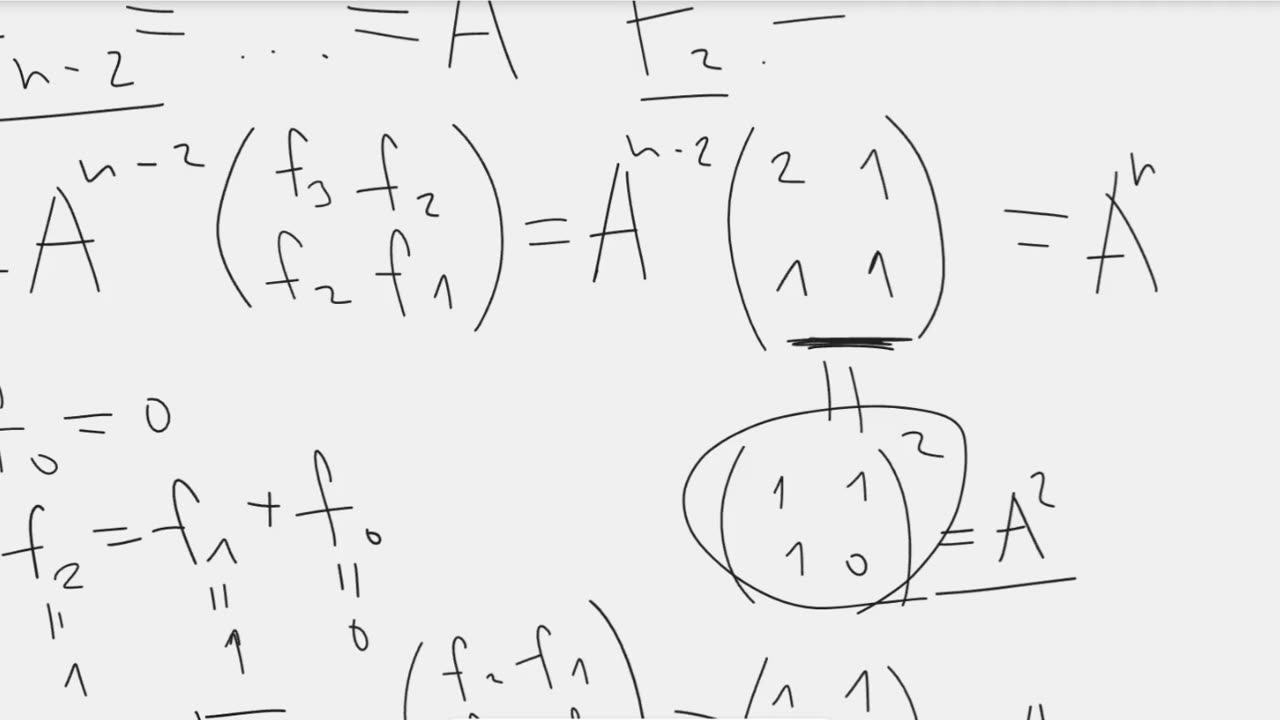
Cassini's identity for the Fibonacci numbers using matrices

5 months ago
21
Science mathematics Cassini Fibonacci Fibonacci numbers matrix algebra identity

Episode 22.

Cassini's identity for the Fibonacci numbers using matrices.
Cassini's identity. For the Fibonacci numbers $f_n$, the following identity holds: $f_{n-1}f_{n+1}-f_n^2=(-1)^n$.
The video contains the proof of this identity using matrices.

The same video on YouTube:
https://youtu.be/JLLIyUVVExU

The same video on Telegram:
https://t.me/mathematical_bunker/46

Loading comments...