Premium Only Content
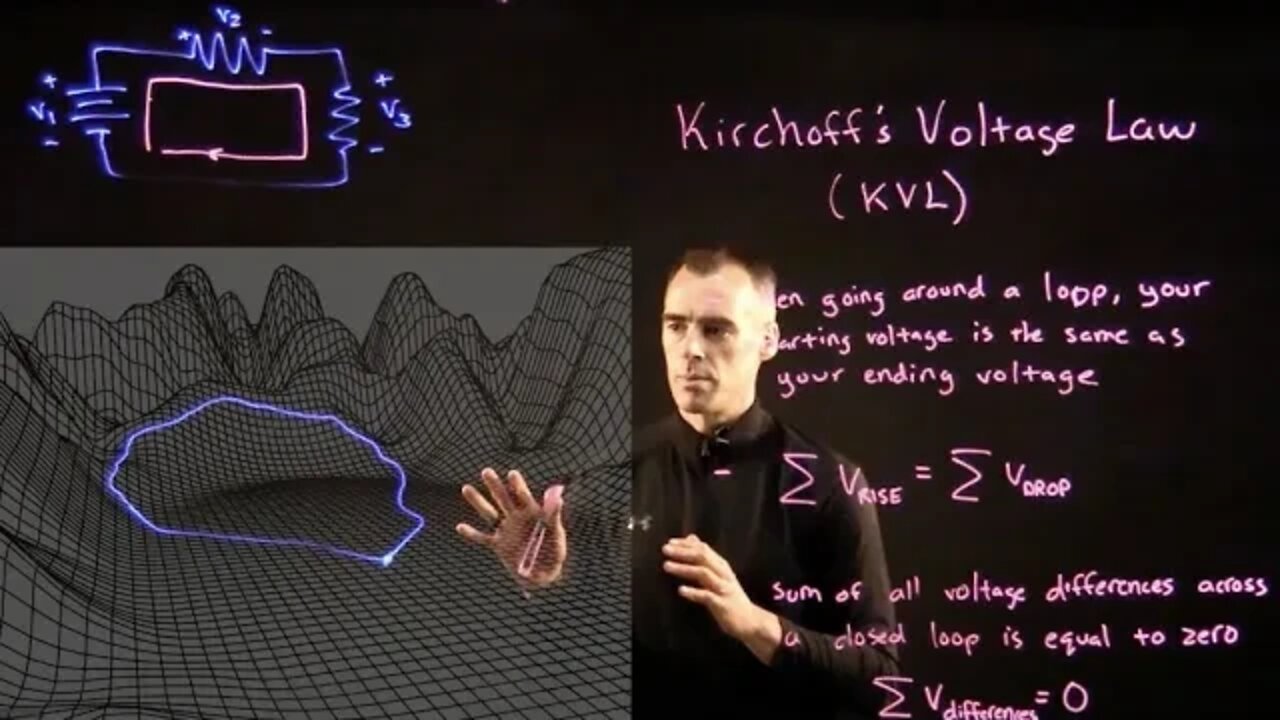
Introduction to Kirchhoff's Voltage Law
Basic explanation of Kirchoff's Voltage Law by analogy to elevation while taking a hike. Below is the script:
Imagine you are hiking this terrain here. Say the trail head is here, you go out to one of the peaks, head back down a different way, then go back down. You could call that trail a 'closed loop'.
Something obvious here is that when you get back, you are at the same place you started, which is at the same elevation. This is analogous to electric circuits.
Say we have a circuit here. If I make a closed loop around the circle, I come back to the place I started, This place has a certain electric potential, which is of course the same whether you're starting or ending here.
This is the basis of Kirchoff's Voltage law, which states:
When going around a loop, you have to get back to the same voltage you started from, or
Sum of voltage rises = sum of voltage drops, or
∑Vrise= ∑Vdrop
By analogy to this trail, the elevation you gain going up the hill, you drop the same elevation when going back down to the hill to your starting place, or another way to say it is:
Sum of all voltage differences around any closed loop is zero, or
By analogy you can sum up all the elevation changes across your hike, and if going up is positive and going down is negative, they will cancel each other out
There are just a few things to be careful about with this analogy. On a hike you might go up a hill and then back the same way you came, but say we are applying KVL in an electric circuit like this,
You are not going to go out and back. This is because in a DC circuit, current will be flowing in one direction only. So you can't pass through the same node twice. Current has to go around.
-
 LIVE
LIVE
Film Threat
23 hours agoSINNERS + CRONENBERG'S THE SHROUDS + TONS OF REVIEWS | Film Threat Livecast
188 watching -
 LIVE
LIVE
Tudor Dixon
3 hours agoWalking with Jesus: A Holy Week Journey with Jeff Cavins | The Tudor Dixon Podcast
220 watching -
 1:04:20
1:04:20
VINCE
3 hours agoSomething Serious Is Going On Behind The Scenes | Episode 25- 04/18/25
156K214 -
 LIVE
LIVE
Caleb Hammer
1 hour agoFinancial Audit’s Thirstiest Guest
188 watching -
 1:16:25
1:16:25
The Big Mig™
5 hours agoEx-CIA & Founder of Panquake, John Kiriakou
20.1K3 -
 LIVE
LIVE
Viss
2 hours ago🔴LIVE - Taking Wins all Over The PUBG Battleground!
155 watching -
 6:23
6:23
Talk Nerdy Sports - The Ultimate Sports Betting Podcast
2 hours agoGood Friday, Bad News for the Books: Riste’s Cold-Blooded Card
7.99K2 -
 1:04:25
1:04:25
Randi Hipper
2 hours agoXRP ABOUT TO SHOCK YOUR PORTFOLIO! MAJOR RIPPLE NEWS
19.3K2 -
![Tulsi Gabbard Declassifies Biden Admin Docs Targeting ‘Domestic Terrorism’[EP 4524-8AM]](https://1a-1791.com/video/fww1/e3/s8/1/Z/7/-/C/Z7-Cy.0kob-small-Tulsi-Gabbard-Declassifies-.jpg) LIVE
LIVE
The Pete Santilli Show
5 hours agoTulsi Gabbard Declassifies Biden Admin Docs Targeting ‘Domestic Terrorism’[EP 4524-8AM]
1,138 watching -
 1:00:49
1:00:49
2 MIKES LIVE
3 hours agoTHE MIKE SCHWARTZ SHOW with DR. MICHAEL J SCHWARTZ 04-18-2025
19.7K