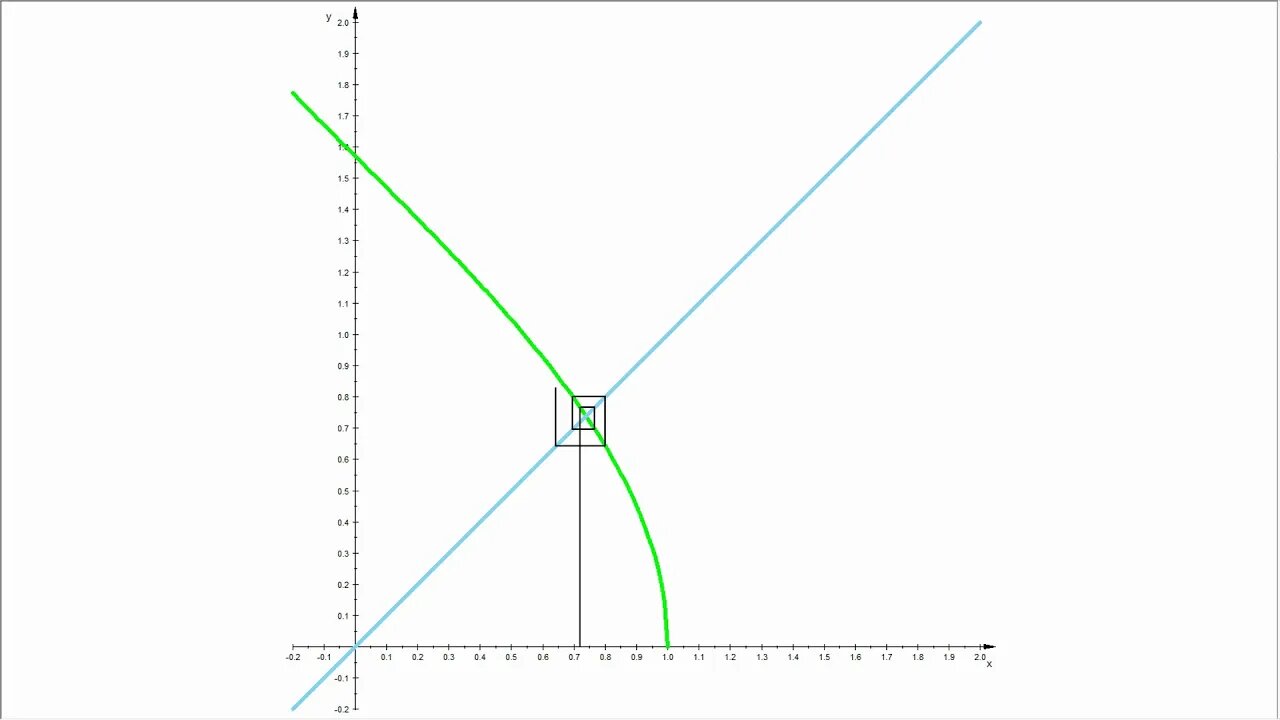
Fixpunktiteration ►Gegenbeispiel Arkuskosinus (nur Animation ohne Erklärung, siehe Videobeschreib.)

In diesem Gegenbeispiel (arccos) werden die Rechtecke größer anstatt kleiner, d.h. die Fixpunktiteration findet den Fixpunkt nicht. Es existiert aber genau ein Fixpunkt? Die Frage lautet daher: Warum funktioniert die Fixpunktiteration nicht? Weil der Banachsche Fixpunktsatz eine hinreichende aber keine notwendige Bedingung für genau einen Fixpunkt ist. Das bedeutet, dass auch wenn der Fixpunktsatz von Banach versagt (mind. eine Bedingung nicht erfüllt), trotzdem ein eindeutiger Fixpunkt vorhanden sein kann, wie das Beispiel zeigt. Mit anderen Worten: Wenn die Bedingungen des Banachschen Fixpunktsatzes nicht erfüllt sind, dann können Fixpunkte vorhanden sein, oder auch nicht.
-----------------------------------
2. Anmerkung: Für eigene Versuche: Ihr müsst die Iteration in der Nähe des Fixpunktes beginnen lassen, weil der Definitionsbereich nur zwischen -1 und 1 liegt.
-----------------------------------
3. Anmerkung:
Betrachtet man die ähnliche Funktion arccos(x)/2, dann sind die Bedingungen des Banachschen Fixpunktsatzes erfüllt (die Ungleichung), und die Fixpunktiteration funktioniert.
-----------------------------------
Kanalmitgliedschaft:
https://www.youtube.com/channel/UCiT0SUtIWTQZQd1galJ-hpw/join
Linklisten:
Es existieren viele Linklisten im Web, z.B. hier: http://www.mathematik.net