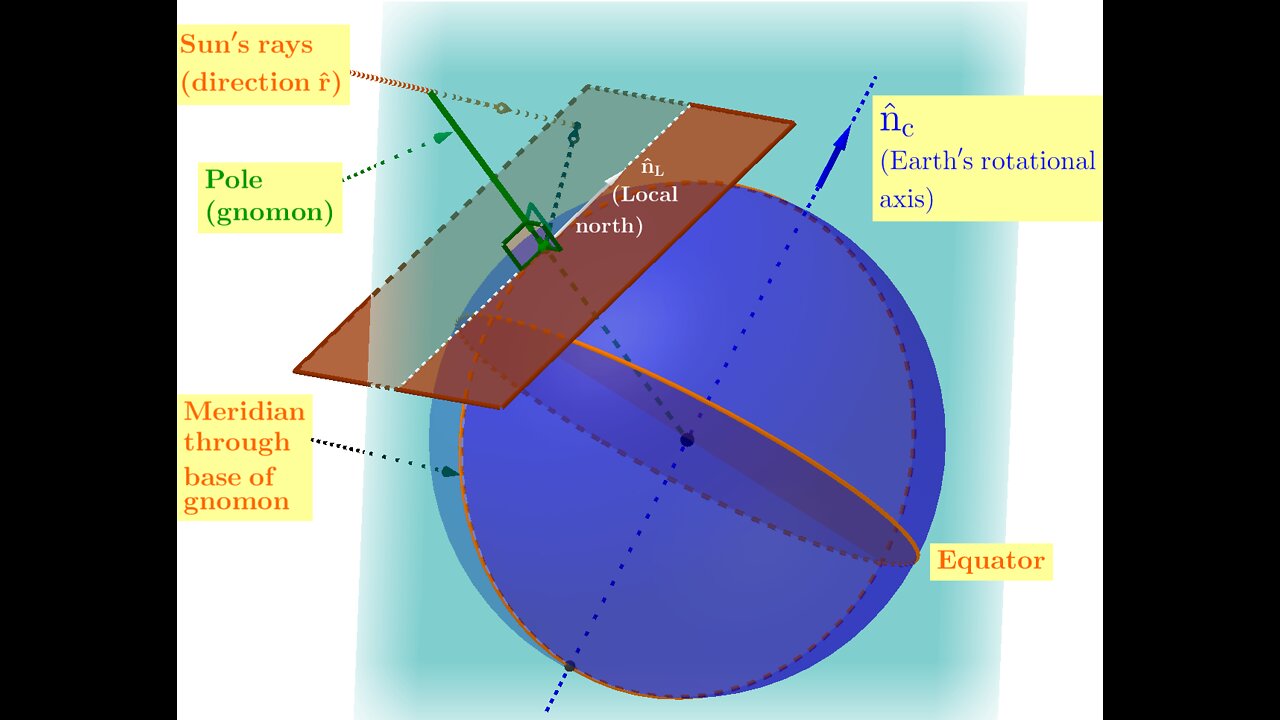
Geometric Algebra: Heliocentric Earth Motion, Gnomons, and Solar Azimuth/Altitude

The paper that's presented in this video is available at http://vixra.org/abs/1804.0363, https://drive.google.com/open?id=1l_Vanm8XObIMH2N0C7TYNGnZ6TAz8q0R
It's discussed at https://www.linkedin.com/groups/8278281

Abstract:
Because the shortage of worked-out examples at introductory levels is an obstacle to widespread adoption of Geometric Algebra (GA), we use GA to calculate Solar azimuths and altitudes as a function of time via the heliocentric model. We begin by representing the Earth's motions in GA terms. Our representation incorporates an estimate of the time at which the Earth would have reached perihelion in 2017 if not affected by the Moon's gravity. Using the geometry of the December 2016 solstice as a starting point, we then employ GA's capacities for handling rotations to determine the orientation of a gnomon at any given latitude and longitude during the period between the December solstices of 2016 and 2017. Subsequently, we derive equations for two angles: that between the Sun's rays and the gnomon's shaft, and that between the gnomon's shadow and the direction "north" as traced on the ground at the gnomon's location. To validate our equations, we convert those angles to Solar azimuths and altitudes for comparison with simulations made by the program Stellarium. As further validation, we analyze our equations algebraically to predict (for example) the precise timings and locations of sunrises, sunsets, and Solar zeniths on the solstices and equinoxes. We emphasize that the accuracy of the results is only to be expected, given the high accuracy of the heliocentric model itself, and that the relevance of this work is the efficiency with which that model can be implemented via GA for teaching at the introductory level. On that point, comments and debate are encouraged and welcome.