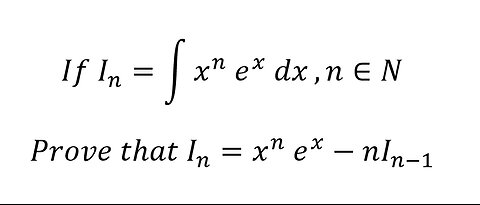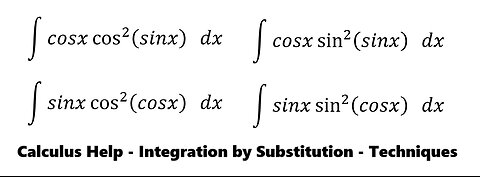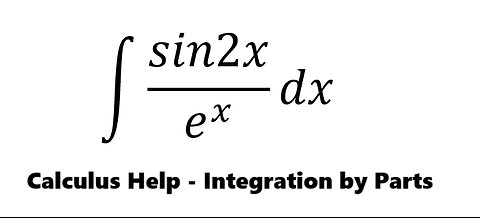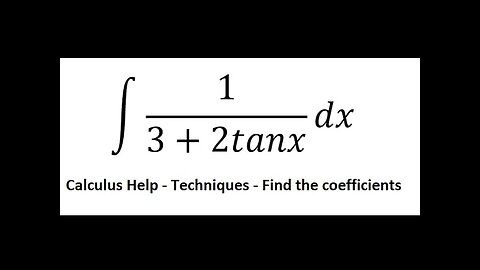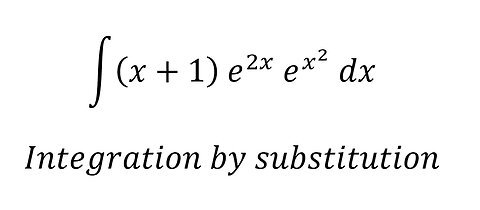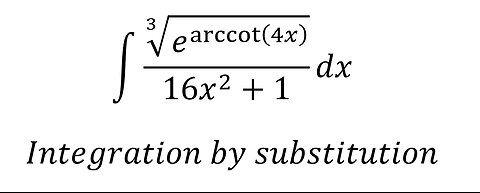-
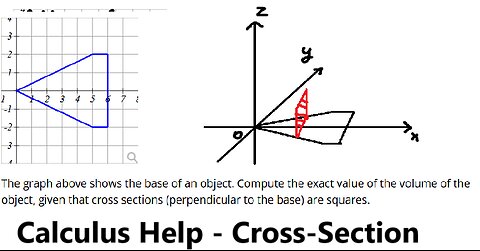
The graph above shows the base of an object. Compute the exact value of the
 saxi753The graph above shows the base of an object. Compute the exact value of the volume of the object, given that cross sections (perpendicular to the base) are squares. #CrossSection #Area #Volume #Integrals19 views
saxi753The graph above shows the base of an object. Compute the exact value of the volume of the object, given that cross sections (perpendicular to the base) are squares. #CrossSection #Area #Volume #Integrals19 views -
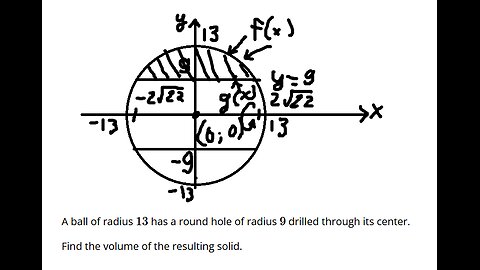
Calculus Help: A ball of radius 13 has a round hole of radius 9 drilled through its center.
 saxi753A ball of radius 13 has a round hole of radius 9 drilled through its center. #Radius #Calculus #Integral #Volume #Integrations31 views
saxi753A ball of radius 13 has a round hole of radius 9 drilled through its center. #Radius #Calculus #Integral #Volume #Integrations31 views -
Calculus Help: Calculus Help: If I_n=∫ x^n e^x dx ,n∈NProve that I_n=x^n e^x-nI_(n-1) #Parts
 saxi753Calculus Help: If I_n=∫ x^n e^x dx ,n∈NProve that I_n=x^n e^x-nI_(n-1) #Parts #Integrals #Techniques26 views
saxi753Calculus Help: If I_n=∫ x^n e^x dx ,n∈NProve that I_n=x^n e^x-nI_(n-1) #Parts #Integrals #Techniques26 views -
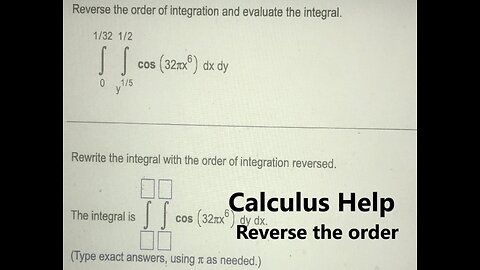
Calculus Help: Reverse the order with the order of integration and evaluate ∫ ∫ cos(32π x^6) dx dy
 saxi753#DoubleIntegrals #Integrations #Reversed #Calculus11 views
saxi753#DoubleIntegrals #Integrations #Reversed #Calculus11 views -
Calculus Help: An object of mass m is dropped into the sea at the surface. It is subject to a
 saxi753An object of mass m is dropped into the sea at the surface. It is subject to a constant gravitational acceleration g and water resistance. (a) (4 points) If the water resistance is proportional to the object's velocity v(t) with coefficient b ≫ 0, so that Newton's second law gives b dv/dt =g- b/m v show that the object's velocity as a function of time t is given by v(t) = mg/b (1-e^(-bt/m)). We take downward to be the positive direction and the object is at rest when it is dropped at t=0. (b) (4 points) If instead the water resistance is quadratic in the velocity, so that Newton's second law gives dv/dt =g- b/m v^2 dt m dv dt find the object's velocity as a function of time t, again assuming that the object is dropped from rest. [Hint: Write Newtons' law as = g(1 − k^2v^2) where k = √b/mg. Then the algebra is a little less messy. After obtaining the final answer in terms of k, remember to replace k by √b/mg.] (c) (2 points) If the object could fall forever under these conditions without hitting the bottom, show that as t→ ∞ the velocity in part (a) approaches terminal velocity v → mg/b. What terminal velocity does the velocity in part (b) approach? #CalculusHelp #Integrals #differentialequations #PartialFractions56 views
saxi753An object of mass m is dropped into the sea at the surface. It is subject to a constant gravitational acceleration g and water resistance. (a) (4 points) If the water resistance is proportional to the object's velocity v(t) with coefficient b ≫ 0, so that Newton's second law gives b dv/dt =g- b/m v show that the object's velocity as a function of time t is given by v(t) = mg/b (1-e^(-bt/m)). We take downward to be the positive direction and the object is at rest when it is dropped at t=0. (b) (4 points) If instead the water resistance is quadratic in the velocity, so that Newton's second law gives dv/dt =g- b/m v^2 dt m dv dt find the object's velocity as a function of time t, again assuming that the object is dropped from rest. [Hint: Write Newtons' law as = g(1 − k^2v^2) where k = √b/mg. Then the algebra is a little less messy. After obtaining the final answer in terms of k, remember to replace k by √b/mg.] (c) (2 points) If the object could fall forever under these conditions without hitting the bottom, show that as t→ ∞ the velocity in part (a) approaches terminal velocity v → mg/b. What terminal velocity does the velocity in part (b) approach? #CalculusHelp #Integrals #differentialequations #PartialFractions56 views -
Integral: ∫ cosx cos^2 (sinx)dx ∫ sinx cos^2 (cosx) dx ∫ cosx sin^2 (sinx)dx ∫sinx sin^2(cosx)dx
 saxi753Here is the technique to solve these 4 integrals by integration by substitution ∫ cosx cos^2 (sinx) dx ∫ sinx cos^2 (cosx) dx ∫ cosx sin^2 (sinx) dx ∫ sinx sin^2 (cosx) dx #CalculusHelp #Integral #Integrations #IntegrationbySubstitution #Substitution37 views
saxi753Here is the technique to solve these 4 integrals by integration by substitution ∫ cosx cos^2 (sinx) dx ∫ sinx cos^2 (cosx) dx ∫ cosx sin^2 (sinx) dx ∫ sinx sin^2 (cosx) dx #CalculusHelp #Integral #Integrations #IntegrationbySubstitution #Substitution37 views -
Calculus Help: Integral ∫ sin2x/e^x dx - Integration by parts - Techniques
 saxi753Calculus Help: Integral ∫ sin2x/e^x dx - Integration by parts - Techniques #Integral #Integrations #Calculus #Formula #Parts35 views
saxi753Calculus Help: Integral ∫ sin2x/e^x dx - Integration by parts - Techniques #Integral #Integrations #Calculus #Formula #Parts35 views -
Calculus Help: Integral ∫ 1/(3+2tanx) dx - Find the coefficient - Integration by substitution
 saxi753Calculus Help: Integral ∫ 1/(3+2tanx) dx - Find the coefficient - Integration by substitution #Integral #Integrations #Calculus #Antiderivative38 views
saxi753Calculus Help: Integral ∫ 1/(3+2tanx) dx - Find the coefficient - Integration by substitution #Integral #Integrations #Calculus #Antiderivative38 views -
Calculus Help: Integral ∫ (x+1) e^2x e^(x^2 ) dx - Integration by substitution
 saxi753Calculus Help: Integral ∫ (x+1) e^2x e^(x^2 ) dx - Integration by substitution #Calculus #Integral #Integrations #Substitution20 views
saxi753Calculus Help: Integral ∫ (x+1) e^2x e^(x^2 ) dx - Integration by substitution #Calculus #Integral #Integrations #Substitution20 views -
Calculus Help: Integral ∫ ∛(e^arccot(4x) )/(16x^2+1) dx - Integration by substitution
 saxi753∫▒〖∛(e^arccot(4x) )/(16x^2+1) dx〗 Integration by substitution #Integration #Calculus #Substitution #Techniques29 views
saxi753∫▒〖∛(e^arccot(4x) )/(16x^2+1) dx〗 Integration by substitution #Integration #Calculus #Substitution #Techniques29 views