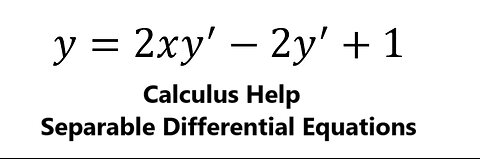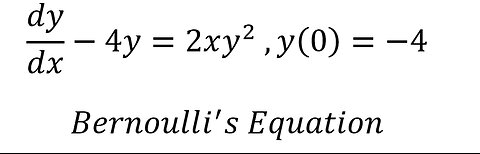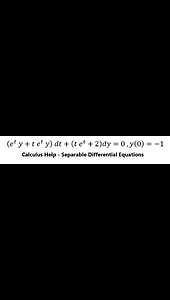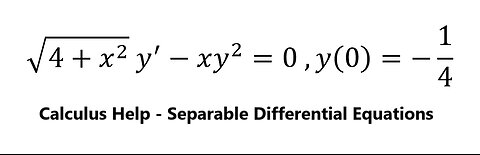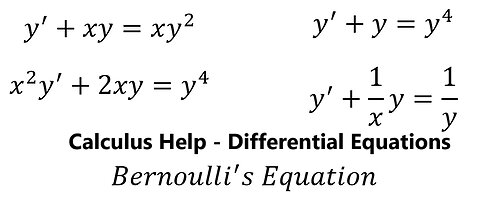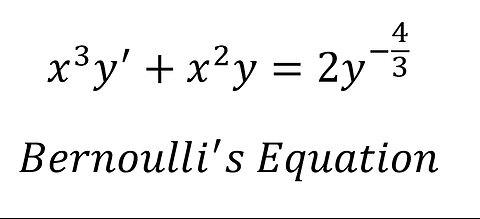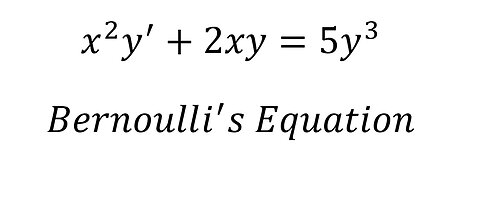-
Calculus Help: Separable Differential equations - y=2xy'-2y'+1 - Techniques
 saxi753Separable Differential equations - y=2xy'-2y'+1 - Techniques #separabledifferentialequations #differentialequation20 views
saxi753Separable Differential equations - y=2xy'-2y'+1 - Techniques #separabledifferentialequations #differentialequation20 views -
Calculus Help: Bernoulli's Equations - dy/dx-4y=2xy^2 ,y(0)=-4
 saxi753Calculus Help: Bernoulli's Equations - dy/dx-4y=2xy^2 ,y(0)=-4 #BernoulliEquations #Equations #CalculusHelp12 views
saxi753Calculus Help: Bernoulli's Equations - dy/dx-4y=2xy^2 ,y(0)=-4 #BernoulliEquations #Equations #CalculusHelp12 views -
Calculus Help: Separable Differential Equations: (e^t y+t e^t y) dt+(t e^t+2)dy=0 ,y(0)=-1
 saxi753(e^t y+t e^t y) dt+(t e^t+2)dy=0 ,y(0)=-1 #SeparableDifferentialEquations #DifferentialEquations #CalculusHelp #Techniques9 views
saxi753(e^t y+t e^t y) dt+(t e^t+2)dy=0 ,y(0)=-1 #SeparableDifferentialEquations #DifferentialEquations #CalculusHelp #Techniques9 views -
Calculus Help: Separable Differential Equations: √(4+x^2 ) y^'-xy^2=0 ,y(0)=-1/4
 saxi753Calculus Help: Separable Differential Equations: √(4+x^2 ) y^'-xy^2=0 ,y(0)=-1/4 #SeparableDifferentialEquations #DifferentialEquations41 views
saxi753Calculus Help: Separable Differential Equations: √(4+x^2 ) y^'-xy^2=0 ,y(0)=-1/4 #SeparableDifferentialEquations #DifferentialEquations41 views -
Calculus Help: An object of mass m is dropped into the sea at the surface. It is subject to a
 saxi753An object of mass m is dropped into the sea at the surface. It is subject to a constant gravitational acceleration g and water resistance. (a) (4 points) If the water resistance is proportional to the object's velocity v(t) with coefficient b ≫ 0, so that Newton's second law gives b dv/dt =g- b/m v show that the object's velocity as a function of time t is given by v(t) = mg/b (1-e^(-bt/m)). We take downward to be the positive direction and the object is at rest when it is dropped at t=0. (b) (4 points) If instead the water resistance is quadratic in the velocity, so that Newton's second law gives dv/dt =g- b/m v^2 dt m dv dt find the object's velocity as a function of time t, again assuming that the object is dropped from rest. [Hint: Write Newtons' law as = g(1 − k^2v^2) where k = √b/mg. Then the algebra is a little less messy. After obtaining the final answer in terms of k, remember to replace k by √b/mg.] (c) (2 points) If the object could fall forever under these conditions without hitting the bottom, show that as t→ ∞ the velocity in part (a) approaches terminal velocity v → mg/b. What terminal velocity does the velocity in part (b) approach? #CalculusHelp #Integrals #differentialequations #PartialFractions56 views
saxi753An object of mass m is dropped into the sea at the surface. It is subject to a constant gravitational acceleration g and water resistance. (a) (4 points) If the water resistance is proportional to the object's velocity v(t) with coefficient b ≫ 0, so that Newton's second law gives b dv/dt =g- b/m v show that the object's velocity as a function of time t is given by v(t) = mg/b (1-e^(-bt/m)). We take downward to be the positive direction and the object is at rest when it is dropped at t=0. (b) (4 points) If instead the water resistance is quadratic in the velocity, so that Newton's second law gives dv/dt =g- b/m v^2 dt m dv dt find the object's velocity as a function of time t, again assuming that the object is dropped from rest. [Hint: Write Newtons' law as = g(1 − k^2v^2) where k = √b/mg. Then the algebra is a little less messy. After obtaining the final answer in terms of k, remember to replace k by √b/mg.] (c) (2 points) If the object could fall forever under these conditions without hitting the bottom, show that as t→ ∞ the velocity in part (a) approaches terminal velocity v → mg/b. What terminal velocity does the velocity in part (b) approach? #CalculusHelp #Integrals #differentialequations #PartialFractions56 views -
Calculus Help: Separable Differential Equations - (1+y^2 )dx+(1+x^2 )dy=0
 saxi753Calculus Help: Separable Differential Equations - (1+y^2 )dx+(1+x^2 )dy=0 #DifferentialEquations #Calculus #Separable #Techniques #CalculusHelp34 views
saxi753Calculus Help: Separable Differential Equations - (1+y^2 )dx+(1+x^2 )dy=0 #DifferentialEquations #Calculus #Separable #Techniques #CalculusHelp34 views -
Bernoulli Differential Equations: y'+xy=xy^2 , x^2 y'+2xy=y^4 , y'+y=y^4 , y'+1/x y=1/y - SOLVED!!!
 saxi753Bernoulli Differential Equations: y'+xy=xy^2 , x^2 y'+2xy=y^4 , y'+y=y^4 , y'+1/x y=1/y - SOLVED!!! #Bernoulli #BernoulliDifferentialEquations #DifferentialEquations #Calculus #Techniques113 views
saxi753Bernoulli Differential Equations: y'+xy=xy^2 , x^2 y'+2xy=y^4 , y'+y=y^4 , y'+1/x y=1/y - SOLVED!!! #Bernoulli #BernoulliDifferentialEquations #DifferentialEquations #Calculus #Techniques113 views -
Calculus Help: Bernoulli's Equations - x^3 y'+x^2 y=2y^(-4/3) - Techniques - SOLVED!!!
 saxi753Calculus Help: Bernoulli's Equations - x^3 y'+x^2 y=2y^(-4/3) - Techniques - SOLVED!!! #Bernoulli #BernoulliEquation #DifferentialEquations29 views
saxi753Calculus Help: Bernoulli's Equations - x^3 y'+x^2 y=2y^(-4/3) - Techniques - SOLVED!!! #Bernoulli #BernoulliEquation #DifferentialEquations29 views -
Calculus Help: Bernoulli's Differential Equations - x^2 y'+2xy=5y^3 - Techniques
 saxi753x^2 y'+2xy=5y^3 Bernoulli' s Equation #BernoulliEquation #Bernoulli #DifferentialEquations #LinearODE21 views
saxi753x^2 y'+2xy=5y^3 Bernoulli' s Equation #BernoulliEquation #Bernoulli #DifferentialEquations #LinearODE21 views -
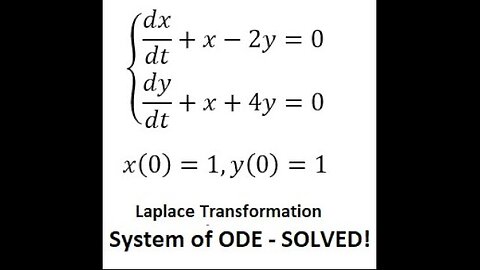
Laplace Transformation - System of Differential Equations: dx/dt+x-2y=0, dy/dt+x+4y=0, x(0)=1,y(0)=1
 saxi753Laplace Transformation - System of Differential Equations: dx/dt+x-2y=0, dy/dt+x+4y=0, x(0)=1,y(0)=1 #LaplaceTransformation #DifferentialEquations #Calculus #Techniques #ToanCaoCap #ToanGiaiTich25 views
saxi753Laplace Transformation - System of Differential Equations: dx/dt+x-2y=0, dy/dt+x+4y=0, x(0)=1,y(0)=1 #LaplaceTransformation #DifferentialEquations #Calculus #Techniques #ToanCaoCap #ToanGiaiTich25 views